уравнения (1.60) можно написать

(г - s) п sin и = (г - s) п Sin и;

{г - So) ii а = (г - So) па.

Перемножив соответственные части последних трех уравнений, получим

паsin ubs - па sin u8s - па {г So)D. (J-64)

Правую часть можно видоизменить следующим образом:

па{r - s)D = n~{r - s,)D = nrh - ) D = nriD,

где to - угол, образуемый параксиальным лучом с нормалью. Тогда уравнение (1.64) принимает вид

па sin u8s - па sin ц 6s - miD. (1.65)

Если написать уравнение (1.65) для всех р поверхностей системы и просуммировать все уравнения, то в левой части остаются только два члена:

прар sin lipbsp - /hai sin «iSsi = rnJ-OKK-

Преобразуем теперь величину D к удобному для вычисления виду: D = sin и - sin и - sin Г + sin ;;

, . с, и - и и ч- и sin и - sin « = 2 Sin----COS---;

поэтому

sin i - sin i = 2 sin -w- COS

и - a = I - (,

D = 2 Sin I cos

u + (( i -\ - i\

--COS-,- ) =

= - 4 Sin -- sill----~--Sin---

Окончательно

= -4 sin -- sin sin --

-npttp sin Upbsp = 4 > гкпкк)к sin - sin ~ sin

(1.66)

. (1.67)

йличина 6si принята равной нулю, что практически всегда имеет-

Иногда удобнее заменить произведение пЧк более симметричным выражением согласно уравнению

««+1 - "к

которое может быть выведено следующим образом:

«к 11 - а, = 10к - ioK = hK ~ hK -

Отсюда

ак+1 - o-ic

Пк+1 - "к

1 г

(1.68)

Введем для краткости символ Аббе

А/= /-/,

где / - некоторая функция величин, относящихся к падающему лучу; / - та же функция координат преломленного луча. Например,

а -а = Да; п п

Теперь можно переписать формулу (1.67) в виде

8sp =

-sm-sin

. (1.69)

Если.одна из поверхностей с номером с - плоская, то соответствующий член суммы принимает вид cxd Х 0. Неопределенность легко раскрыть, так как произведение sin- стремится к , поэтому слагаемое для поверхности с принимает более простой вид

(1.70)

1 Лас c-c .

sin-sin

и. + и„

Кербером выведена подобная же формула, дающая отступление от закона синусов, т. е. величину, позволяющую определить кому системы для точек, лежащих достаточно близко от оси (см. стр. i у)-

Пусть угловое увеличение системы равно

Обозначим

знаком б (sin и) следующее выражение:

б (sin Uk) = sin Up - sin

Формула Кербера для отступления от закона синусов имеет вид

Л (sin Up)

sm и.

причем

(1.71)

(1.71*)

где / = s sin U - длина перпендикуляра, опущенного из вершины поверхности на луч; таким образом, 1 = sj sin и; - высота падения параксиального луча на к-ю поверхность стгстемы; d - расстояние между поверхностями с номерами к и /с+1; - величина, определяемая формулой (1.66). *

Вывод формул (1.71) и (1.71*), практически мало применяемых вследствие их сложности, приведен в книге Рора[1 ] на стр. 305- 307.

При вычислениях надо обратить внимание на то, что в формуле (1.71*) под вторым знаком суммы происходит .цвойное суммирование, так как величина бз сама получается согласно формуле (1.69) в результате суммирования по первым к поверхностям.

Разностные формулы для внеосевых пучков

Г. Д, Рабиновичем [71 предложена очень простая и удобная формула для вычисления отступления от отношения синусов. Дальше (гл. И) будет показано, что важной для оценки комы

оптической системы является величина 11=-- + -,-, где

V x - s

V - поперечное увеличение системы. Величина г может быть

получена в виде суммарной формулы

пР (х - s) sin и

Развернутое выражение для D дано формулой (1.66). Вывод этой формулы основан на формуле (1.64). В выводе формулы (1.64)

{•прлается предположения, что действительный и параксиальный «и исходят из одной и той же точки на оси системы. Заменяем пвый параксиальный луч вторым с величинами я х, ъ деи-вительньГй луч оставляем прежним, исходящим из центра предмета. Соотношение (1.64) принимает вид

пР sin и (s - x) - "Л sin «1 (si - xi) =

V v>

где s и s - координаты точек пересечения действительного луча с осью до и после преломления.

Имеем .Sj - s,; s s + Л.ч; следовательно,

/гР sin и {$ - х) - /tiPi sin «j (sj - xj) =

fs+ Дх-x Pi (si - xj) hi sin ttj

= nP sinw (s - x)

(1.73)

s-x f, ~n sin kj

Ho так как

"llPl (-i - i) = {x - s) = ~\-J,

где / - инвариант Лагранжа-Гельмгольца, то

(si - xi) na j 5 (s - x) itipLi ~ V

С другой стороны, по определению

п sin а

Подставляя два последних равенства в уравнение (1.69) и используя выражение для г\, получаем

аР sin и (s - х) - /tPi sin (s - х) =

. nfV sin W (s - x) I + -z:y " = -fipsin«(s -x)n-

Из этой формулы легко получить окончательную формулу (1-72). Г. д. Рабиновичем [7] выведена еще одна формула, kotoj рая может быть полезна при расчете аберраций наклонных луЧ№ в меридиональной плоскости, а именно:

cos ц-cos «1 cos и

na cos и

(1.74) 41

где D - рассмотренная раньше величина, представляющая собой выражение D = sin и - sin и - sin i + sin t.

Углы «, i, i относятся к рассматриваемому лучу.

Этой формуле можно еще придать вид

А/ =

п а cos и

- na/j (cos - cos u)

(1.74*)

A/ = -

re a cos и

v=p v=l

--D, + 2«,aAsinXL Sin

Если Si = OO, формула (1.74*) принимает вид

1 dy

М = l + figwi

па cos и

cos и

(cosu - cos«).

в последних формулах отдельные слагаемые характеризуют влияние каждой поверхности.

Разностные формулы Кербера-Рабиновича целесообразно применять при расчете очень длиннофокусных объективов, например объективов астрономических труб, когда основной тригонометрический расчет хода лучей необходимо выполнять при помощи семизначных таблиц логарифмов. Дифференциальные формулы позволяют получить ту же точность в величине аберраций при использовании пятизначных таблиц логарифмов как прн расчете хода луча, так и при вычислении самих аберраций по формулам (1.67), (I.7I) или (1.72). Особого выигрыша во времени эти формулы, однако, не дают, так как необходимо сначала рассчитать ход луча с пятизначными таблицами, а затем произвести все вычисления по формулам (1.69), (I.7I) и (1.72). Ценность дифференциальных формул заключается в том, что они дают возможность определить отдельно влияние каждой поверхности на аберрации.

В настоящее время дифференциальные формулы применяются мало, так как при точности выполняемых на современнных ЭВМ вычислений нет нужды в специальных приемах. Тем не менее приведенные выше дифференциальные формулы представляют теоретический интерес: они, например, позволяют оценить влияние аберраций высших порядков и их распределение по поверхностям, и решить ряд других задач.

Разностные формулы для волновой аберрации

Для оценки качества изображения, даваемого оптической системой, необходимо (см. гл. X) знать величину волновой аберрации, т. е. отступления поверхности волны (поверхности, ортогональной лучам пучка, выходящего из оптической системы и образующего изображение точки-предмета) от идеальной (сферической) волны.

Рассмотрим частный случаи, когда точка и ее изображение находятся на оси оптической системы. Пусть S ipiic. I.I5) -

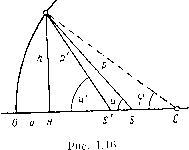Рис. 1.15

точка, из которой исходит луч 5М,. После выхода из системы луч пересекает ось ее в точке 5. Обозначим через pi расстояние SMi (на чертеже отрицательное); через dj - расстояние по лучу от первой до второй поверхности; через - расстояние по лучу от /с-й до к + 1-й поверхности. Величина -/hPi + f-di • • •+ -j-np = / называется оптическим путем луча. Если из этой величины / вычесть сумму -nSi - n.jdi + + ns ~ /о (оптический путь вдоль оси системы), то разность I - 1 обозначает волновую аберрацию луча SMj. Эта разность I - 1, как показал Конради, может быть вычислена при помощи приема, аналогич- ного приему, примененному Кербером для вывода его дифференциальных формул. Вычислим разность / - 1» для одной поверхности. В этом случае (рис. 1.16)

/ - пр --np - ins - ns) = п (р -s) - n{p--s), (1.75)

sm и

где р =

высоте h. Далее

p~s = h

a - стрелка, соответствующая

sm и

tg и

- a=h

tg ч - sin if sin u tg и

.2гзт2