в правой части рисунка нанесены те точки входного зрачка, через которые проходят лучи. Точки соединены кривыми, одна из которых проходит через край действующей части входного зрачка, вторая подобна первой с коэффициентом подобия 0,7. В левой части

рисунка даны кривые в плоскости изображения. Эти кривые сложны по очертаниям вследствие заметного влияния аберраций высших порядков.

Чаще всего работу ограничивают, изучая подробно отклонения 8g меридиональных лучей, пересекающих плоскость входного зрачка в определенных точках, которые рационально расположить по закону корней квадратных (например, точки Л, Bi, С], . . ., Лд на рис. 11.50). Число точек выбирается таким, чтобы можно было чертить с уверенностью кривую зависимости bg от mj. Обычно требуется от трех до семи точек: три точки в обычных телескопических системах, пять - в фотографических объективах средних и больших апертур, семь - в микроскопах большой апертуры. Пример такого графического изображения зависимости величины б (или /) от mi показан на рис. П.52. Можно на тот же рисунок нанести такие же кривые bg для тех же лучей, но с другой длиной волны, что даст представление о хроматической разности увеличений в зависимости от mi.

Аберрации главных лучей и бесконечно тонких пучков, направленных вдоль этих лучей

Существует группа аберраций, зависящих только от угла поля зрения и не зависящих от апертуры системы: это астигматизм бесконечно тонких пучков и кривизна изображений этими пучками, дисторсия и хроматическая разность увеличений.

Следует представлять графически в виде кривых зависимость каждой из этих четырех аберраций от угла поля или от расстояния предмета (или изображения) от оси, откладывая аберрации по оси абсцисс и углы поля - по оси ординат. Для всех углов w, для которых уже сделаны тригонометрические расчеты хода главных лучей, рассчитывают положения фокусов бесконечно тонких астигматических пучков, осью которых служат главные лучи (mi = Ml = 0).

Расстояния х и х этих двух фокусов (меридионального и сагиттального) от гауссовой плоскости наносятся на координатную сетку как функции от wi, 1\ или 1р. На рис. П.53 даны кривые, полученные таким образом для анастигмата типа триплет. Расстояние между кривыми, обозначенными сплошной и штрих-пунктирной линиями, отсчитываемое параллельно оси абсцисс, дает астигматическую разность, а кривая (на чертеже - штриховая линия), проходящая посередине между ними, - так называемую среднюю кривизну изображения.

Пользуясь этими кривыми, можно исследовать аберрации высших порядков, определив несколько коэффициентов в разложениях поперечных аберраций - из числа тех кoэффициeнJoв, которые содержат одну из величин m или М в первой степени, например коэффициенты и Siv аберраций третьего порядка в формуле (П.58), bi и 6, - аберраций пятого порядка в формуле (П. 163). Характер кривых, приведенных на рис. 11.53, указывает на наличие в разложении величины х членов высших порядков с положительными коэффициентами, обусловливающих быстрое приращение величин х в положительную сторону при возрастании угла W. Еще сложнее обстоит дело с кривой х: два перегиба показывают, что среди коэффициентов разложения имеется не менее двух со знаком минус и одного - со знаком плюс.

Таким же образом можно изображать графически поперечную

дисторсию бд или относительную дисторсию А = 100--г-, выра-

женную в процентах, как функцию от wi или /р (сплошная линия на рис. 11.54). На тот же чертеж можно наносить и хроматическую

разность увеличении -~, которую можно также выражать в про-

центах (штриховая линия на рис. 11.54).

До сих пор не существует единообразия в выборе величины, откладываемой по оси ординат. В большинстве случаев этот выбор безразличен. Если предмет на бесконечности, откладывают обычно hi, которое совпадаете mi; иногда откладывают и, выраженное в радианах и помноженное на 100. Более рационально откладывать sin и, так как с этой величиной связано значение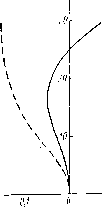

потока, прошедшего через систему. Известно, что для точки на оси поток Ф, прошедший через систему с круглым входным зрачком и падающий на некоторый элемент поверхности ds, равен

пград Ф = nBkds Sin* и,

где В - яркость источника; k - коэффициент прозрачности; и - апертурный угол со стороны изображения.

Аргумент sin и имеет еще то удобство, что он не связан с фокусным расстоянием системы; кроме того, если откладывать величину Г] (см. стр. 213), определяющую кому при аргументе sin и, значение производной позволяет точно вычислить кому для любого малого угла поля.

Аргумент sin и может применяться и в том случае, когда предмет находится на конечном расстоянии. Однако, как будет .oi j,% показано в следующем параграфе, аргумент tg и также имеет преимущества и в неко-Рис. 11.54 торых случаях должен быть предпочтен.

Выбор плоскости наилучшего изображения

Продольные аберрации обычно отсчнтываются от гауссовой плоскости изображения. Однако во многих случаях наименьший кружок рассеяния поперечной аберрации оказывается не в гауссовой плоскости. Выше рассматривалось изменение величины аберрационного кружка с изменением плоскости установки в том случае, когда сферическая аберрация определяется исключительно членом третьего порядка; наименьший кружок рассеяния тогда получается в плоскости, находящейся от гауссовой на расстоянии /As, где As-величина продольной сферической аберрации крайнего луча пучка.

В общем случае, когда помимо члена третьего порядка имеются еще и члены пятого, седьмого и более высоких порядков, вопрос о нахождении наилучшей плоскости установки уже не может быть решен аналитически, но графически решается просто.

Пусть б - поперечная сферическая аберрация для определенного луча, составляющего с осью угол и после выхода из системы; А - расстояние от гауссовой плоскости до некоторой плоскости установки. Ясно, что в новой плоскости установки высота ёд точки пересечения луча с плоскостью равна

Sg-1= 6g -Atgu.

Если величина б нанесена на график (рис. 11.55) как функция от tg и, то, проводя на этом графике прямую, уравнение которой

у = -А tg и, и измеряя по горизонтали расстояние между кривой 8g и прямой, равное бд, получаем картину изменения бд от угла и. Подбирая наклон прямой 0D таким образом, чтобы расстояние между кривой и прямой оказалось минимальным, что легко выполнить на глаз, получаем как положение наилучшей плоскости установки, так и значение остаточной поперечной аберрации в этой плоскости. На рис. 11.55 наилучшая плоскость установки соответствует прямой 0D.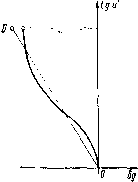

Рис. 11.55

Контроль результатов расчетов

При расчете хода лучей часто встречаются ошибки, не настолько грубые, чтобы сразу обратить на себя внимание, но все-таки несколько изменяющие картину аберраций и потому направляющие конструктора на неверный путь; поэтому ни одна из аберраций, полученных в результате расчета хода лучей, не должна остаться без контроля. Из многих возможных способов контроля остановимся только на интерполяционных способах и способах, основанных на применении теории аберраций.

Интерполяционные способы основаны на изучении при помощи графиков изменений функции при малых изменениях аргумента; все графики аберраций должны давать достаточно плавные кривые. При всей произвольности понятия о «плавности» этот способ в опытных руках является одним из более надежных. Для начинающего этот метод мало пригоден, так как он не исключает ошибок, в особенности систематических, и мало поучителен. Но в сомнительных случаях добавление одной «точки», т. е. результата расчета нового луча, может оказаться весьма полезным.

Применение теории аберраций для контроля результатов тригонометрических расчетов может быть удобным и весьма полезным во многих случаях. Для примера рассмотрим несколько приемов.

1. Зная первую сумму Sj, определяющую сферическую аберрацию третьего порядка, можно проверить ход кривой продольной сферической аберрации 6s как функции от координаты на входном зрачке или от угла падающего луча с осью (о в области, близкой к оси. Пользуясь формулой для продольной сферической аберрации третьего порядка

6s =

2п„а

-q-Si,

(11.241)

следует произвести вычисления для нескольких лучей, пересекающих входной зрачок на небольших высотах, и построить кривую зависимости 6s от (Oj. Сравнивая ее с кривой, построенной на основании тригонометрических расчетов, можно судить о правильности последних.

2. Расчет положения фокуса бесконечно тонкого меридионального пучка может быть проверен, если имеются кривые, дающие зависимость между величиной меридионального отклонения б, полученной путем расчета хода луча через оптическую систему,

и ординатой точки пересечения луча с плоскостью входного* зрачка.

Предположим, что график составлен таким образом (см. рис. П.52), что по оси абсцисс отложены 6 (или ординаты / точек пересечения луча с гауссовой плоскостью изображения), а по оси ординат - величины т. Для составления такого графика требуется расчет хода от трех до пяти лучей.

Угловой коэффициент / касательной к кривой в точке (см. рис.

П.52), для которой mi = 0, равен t = . С другой стороны,

пусть (рис. П.56) РР, SS - линии пересечения меридиональной плоскости с плоскостями выходного зрачка и изображения;

- расстояние от плоскости изображения до фокуса бесконечно тонкого меридионального пучка; PS = s ~ х. Рассмотрим два бесконечно близких меридиональных луча MN и MN2, пересекающихся в фокусе F бесконечно тонкого меридионального пучка; du - угол между лучами MNи MN2, d ig) = 12 ~ приращение 1 при изменении угла и на du; dm = М1М2 - приращение величины т при том же изменении угла и. Тогда из свойств подобия получаем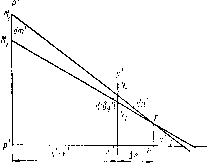

Рис. 11.56

РН ММ

s -х + An

d(bg) dm

Пренебрегая A„j по сравнению с s~ х, можно написать

d{&g)

A = (s-x

dm. •

С другой стороны, полагая dm = dm

- увели-

чение в зрачках, имеем с достаточной степенью точности

A = (s-x)

dj&g) т dm т

Но так как ной, то

= t - угловой коэффициент касатель-

A, = (s-x)/-

(11.242)

Все величины: А„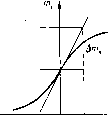

t, -j,--известны. Если равенство (П.242) не удовлетворяется, имеется ошибка либо в вычислении меридионального пучка, либо в вычислении хода одного из лучей, служивших для вычерчивания кривой bg = / (т).

Указанная проверка необходима, когда изучается новая система. Практика показывает, что ошибки в вычислениях положения фокусов меридиональных лучей встречаются

сравнительно часто. Величину t, т. е. К

определяют следующим образом. Проводится касательная к кривой bg в точке т = О (рис. П.57), и определяются две точки пересечения этой касательной с двумя горизонтальными линиями, разность ординат которых равна круглому числу для Am. Измеряют соответствующую разность абсцисс, учитывая, конечно, масштаб.

Отношение -представляет собой величину

3. Кому можно проверить, пользуясь формулой (П.92), приведенной на стр. 117. В наиболее часто встречающихся случаях, когда величина ц мала и мало меняется, удобнее пользоваться более простой формулой

6s \

Рис. 11.57

K=2>L

6 + .

X - S

р р J

Напоминаем, что под К понимается величина

где /о - высота, на которой луч с координатой т\ = О пересекает плоскость изображения; /+т и / т - такие же высоты для двух других лучей. Эту формулу можно написать еще и так:

(11.243)