Замечая, что

cos {i - i) = ХК + fXfX + VV = Vl-(jx2 + v2) /1-(n + v") -f,

+ nii+vv = (I e) 2 (1 e) 2 + + VV,

подставляем это выражение в формулу (11.35). Разлагая в ряд корень квадратный, входящий в эту формулу, и удерживая в разложении необходимое число членов, можно написать в виде

W,rin-n) 1 +

2iin

S + 8 , 8 + 82 - 286

откуда

(n - пГ

(11.36)

Т = {в- - т; {г + в + 2ее - 46 (е + е) 46).

(« - rt)-

Чтобы получить - оптический путь для главных плоскостей, совпадающих и проходящих через точку О, - нужно к прибавить

Wfj - W, = r{nX-nX)==~r{n-n) + rQ,

Q = ~ (пе - пе) + ~ (пе - пе).

Складывая Wc + (Wff - W) = и отбрасывая члены второго порядка, излишние при вычислении аберраций, после простых преобразований получаем

= щ/) [{пг - ту - (е -f е - 26)] , (11.37)

где индекс 4, поставленный у величины \F, означает, что в разложении приняты во внимание только члены, содержащие четвертую степень величин р, v, р и v.

Производя возведение в квадрат, приведение подобных членов, сравнение коэффициентов при разложении W [формула (П.22)] и переходя от коэффициентов а к коэффициентам Ь, получаем, по-

1 П2п2

лагая q:-rjy:

I и 1 (n - n) ,

bz = q\ b i = - ~ q --r,-; b, - q.

Выражения сумм 5 через радиус, показатели и увеличения т и т.

Подставляяэтизначения Ьввыражения(11.31)дляаберраций и разбивая на множители, получаем выражения зейделевых коэффициен-

n - /1

nnr

-Sv = ? -

T (t-1)

(n - ny

{r-ry

(11.39)

Выражения сумм 5 через аир. Для вычислений удобно рассматривать два параксиальных луча, один из которых пересекает оптическую ось в центре плоскости предметов и образует с осью углы «1, «2. • • •. «р, а другой пересекает ось в центре входного зрачка и образует с осью углы Pi, Рг, . . ., р. Эти переменные введены Ланге. Замечая, что

Р 1 пЬг

=Y

2 (п - rt)-

г =--h -г-г

па - па

, Jt ./т («/г - art)

~ rt/aP ~ п;гар/г

(11.40)

где / определяется по формуле (П.30 *), получаем для сумм Зей-деля выражения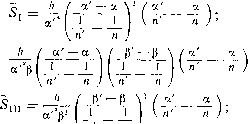

\п п /

1 ап - an

~aps/l i\2\n nja - a

J2 gn-an P -p aph nn a - a

(11.41)

Имея аберрации отдельных поверхностей, можно вычислить аберрации всей системы, перенося поперечную аберрацию, вызванную поверхностью к, в пространство изображений всей системы с помощью закона Лагранжа-Гельмгольца.

Пусть р - номер последней поверхности системы; к - номер произвольной поверхности; тогда napbgp = nabg. Для получения инварианта Лагранжа, относящегося к поверхности с номером к, достаточно помнол<ить формулы (И.ЗО) с обеих сторон на а. Складывая величины nabg, относящиеся ко всем поверхностям, получаем поперечную аберрацию bg всей системы, умноженную на fia; поэтому

- 2npbgp = со; LJ + Qp] V S,« +

-2ПрЮр = р{(0р +

2pQ-pW, V S„, + Qpw\ V (Snv + -l%v\.

(П.42)

Вводил! обозначения S

SjiK П T. д.

Тогда

V " M у

a 1

\ n 1 \ n ]

(П.43)

и г. д.

Заметим, что выражения сумм aSj, «рц, . . . , aS однородны относительно переменных а и (3, т. е. не зависят от выбора

единиц для а и р. Условимся брать = 1; Pi = 1. Тогда выражения для зейделевых коэффициентов принимают вид

S, Ц hP;

1 an - an h nn

(П.44)

/ Да \2

; Да = a - a; Др = p - P;

Д-Л--.

Формулы (И.42) совместно с формулами (П.43) являются основными для расчета оптических систем. Они относятся к общему случаю любых центрированных систем, составленных из сферических поверхностей. В том виде, в котором они приведены, они позволяют вычислить лишь приближенные значения аберраций систем с небольшими апертурными углами и при небольших углах поля. В сущности, они заменяют тригонометрический расчет хода лучей, требуя гораздо меньшей затраты труда (вычисления требуют трех-четырех знаков и во многих случаях могут быть выполнены с помощью логарифмической линейки, в то время как тригонометрический расчет требует применения шестизначных таблиц).

Формулы для коэффициентов аберраций третьего порядка играют настолько важную роль в расчете оптических систем, что необходимо иметь самые разнообразные видоизменения этих формул; на практике представляется большое число отдельных частных случаев, требующих применения тех или иных вариантов формул.

Переписываем формулы (П.42) и (П.44) с учетом формул (И.43):

- 2rt„

- (Optiiii (3Sin + fSi\) + ш?5у;

2ПрШр = Qp [iop + Q; ) Si -f 2щ,0.р w\Sn + Q>US„i + /Siv),

(П.45)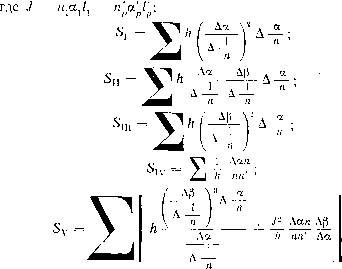

(11.45*)

Как было указано выше, при выводе формул (11.45) предполагалось, что точка-объект лелшт в меридиональной плоскости. Но иногда встречается необходимость иметь формулы, пригодные для общ,его случая, когда положение точки определяется двумя координатами и Lj. Вывод формул для 8g и 6G при (или

Wi = ) отличном от нуля может быть выполнен с помощ,ью

формул (П.45), применяемых для случая, когда меридиональная плоскость повернута на некоторый угол -ф, определяемый формулой tg -ф = ~- . Зная выражения для аберраций в повернутой 1

системе координат, можно получить выражения для их проекций на первоначальные плоскости. Подробный вывод смотри в книге А. И. Тудоровского [13] на стр. 451.

В результате получаются следующие формулы:

- 2np6gp = сОр [Ыр + Qp ) Si + [SwpOip + WpQp +

2Wp<0pQp]Su

P \ Wp

[3wp Cup

iOpWp +2wpWpQp]Sni-i-f wpiwp +Wp]Sy;

-2np6Gp=Qp

(-On

(sV/pQp + Wp + 2uvo;q;) Sii +

3WpQp + Qpp + 2©»;) Siii + -f /Qp [wp + Wp) S,v + Wp (wp + Wp) Sv

(11.46)

Выражения сумм S через * и лг. Приведем формулы (11.46) к виду, предложенному еще Зейделем и Рором. С этой целью заменим углы отрезками, относящимися к пространству предметов. Используем формулы (11.29)

/ , т М

W -

X - S

X - S

Й = -

Затем замечаем, что для параксиального луча

1 1

~)--hQs,

та1< как инвариант --

через Qs.

С другой стороны,

обычно, принято обозначать

п . . ( п , \ . ,

п \ п

поэтому (п откуда

Величина

- и) -V = а - а, или ni =

а. - а

пп =

rt s rts / ns

Аналогично имеем

Кроме того, нужно заменить все величины, относящиеся к пространству изображений (ю, Q), величинами, относящимися к пространству предметов.

Принимая во внимание однородность выражений аберраций относительно величин а и р, а также соотношения

«1 «1 а/

Которые можно считать точными в области аберраций третьего порядка, формулы (11.42), (11.43) и (11.45) можно написать в любом Мде, содержащем величины со и Q вместо со и Q (при условии,