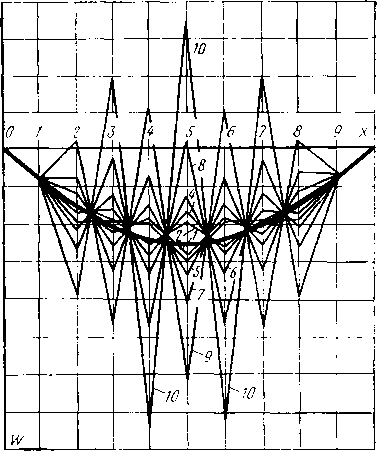Рис. 1.18.

ются погрешности, знак которых в каждом следующем узле изменяется на противоположный. Обратим взимание на графики полученных «приближенных» (решений, показанные на рис. 1.18. Эти графики представляют собой пилообразные линии и в каждом следующем шаге по координате отклоняются от точного решения в противоположную сторону. Более того, в каждом следующем шаге вычислений папрешности изменяют знак. Это чередование знаков погрешностей характерно для неустойчивости по начальным данным.

Нарастание погрешностей в данном случае происходит примерно по закону геометрической прогрессии (рис. 1.19). В каждом

следующем шаге погрешности возрастают примфно в полтора раза. Может быть нопытаться уменьшить шаги сетки /г, чтобы добиться устойчивости?

Нет! Изменение шага приводит лишь к более быстрому возрастанию полрешностей. Рост погрешностей в некоторой степени сдерживается точным заданием значений W на кондах стержня. При измельчении шага сдерживающее PiHc. 1.19. влияние концов уменьшается.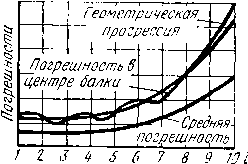

Погрешности будут расти быст1рее, но основание Пропресоии в данном случае не может быть большим 10/6. Цифра «10/6» следует из итерационной формулы (1.17). Если каждое значение w\ входящее в эту формулу, будет содержать некоторую погрешность Л и знаки попрешностей будут изменяться от узла .к узлу, то в результате в следующем приближении погрешность увеличится:

- + А) + Hwm-- А) + 4(Um+i-A)~(m+2+A)

в чем же причина неустойчивости? В данном случае имеется три причины.

Первая состоит в том, что процесс вычислений и формула (1.17) являются рекуррентными. В этой формуле для вычисления каждого следующего приближения использует результаты предыдущего приближения. Цроцесс вычислений от шага к шагу повторяется и происходит накопление погрешностей.

Однако не все рекуррентные процессы вычислении приводят к неустойчивости. Формула (1.12) также была рекуррентной, но Шроцесс вычислений с ее помощью получился устойчивым. Следовательно, ремуррентиость только создает предпосылки для неустойчивости.

Вторая причина - чередование знаков перед членами уравнения и вызывает накопление таких погрешностей, которые имеют такое же чередование зна1кав. Чередование знаков получилось у нас не случайно. При замене дифференциальных уравнений разностными, знаки как правило, чередуются. Например, все разности от первой до четвертой на рис. 1.17 имеют чередующиеся знаки. Чередование знаков получается и при построении разностных формул из физических соо1бражений. Однако это не значит, что формула, в которой знаки перед членами изменяются от узла к узлу, обязательно приведет к неустойчивости. Чередование знаков создает вторую предпосылку для неустойчивости.

Третья причина состоит в том, что сумма коэффициентов перед членами в правой части ф01рмулы (1.17) больше единипы:

1/6 + 4/6+4/6+1/6=10/6.

Если бы эта сумма была меньше единицы, то в любом случае возрастания погрешностей не происходило бы.

Таким образом, неустойчивость имеет три причины и достаточно устранить любую из них, чтОбы решение было устойчивым. Например, можно избежать рекуррентного процесса. Для этого достаточно один раз решить систему нз семи уравнений (1.16) относительно неизвестных прогибов в семи внутренних узлах сет:,п. При этом значения прогибов в узлах получатся точными.

Труднее И31бежать чередования знаков перед членами в разностной формуле, аппроК]СИ1МИ1рующей четвертую производную, чо можно нарушить чередование знаков перед погрешностями в п;>о-цессе расчета.

Например, при вычислении каждого следующего приближения можно использовать значения функций, полученные уже в том приближении.

Попробуем ввесш в расчет это правило. При вычислении значений прогн<бо;В узлы обходятся в направлении возрастания номеров т, прогибы в пройденных узлах т-1, т-2 в очередном приближении уже вычислены и их можно ввести в итерационную формулу

(Ы8)

Если узлы обходят в порядке убывания номеров /п, то вычис-ленныгми в очередном щриближении i+I будут прогибы в узлах m+l. т~2 и т. д. Итерационную формулу в этом случае можно записать в виде

""i}; = 1п2 + «>LVi + - «m-2)/6- (1 • l)

Начнем расчет с теми же начальными значениями прогибав, что ч на рис. 1.18. Будем пользоваться формулами (1.18) и (1.19) поочередно {табл. 1.5). При четных значениях i и направлении обхода

Таблица 1.5

Номер узла т

узлов сле1ва направо используем формулу (1.18), а при нечетных i (направление обхода справа налево) (I.I9).

Результаты вычислений показывают, что в начале расчета (t= •=2) в отдельных узлах погрешности получаются больше первоначальных (рис. 1.20). Но характерного для потери устойчивости чередования знаков погрешностей не наблщдается. В следующих приближениях попреш1Ности быстро уменьшаются, и на 11-м шаге вычислений итерационный процесс сходится. В 12-м ктерационном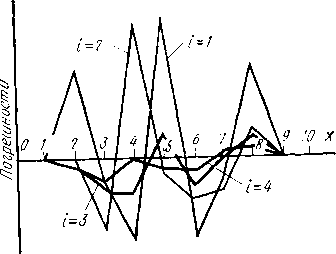

Рис. 1.20.

цикле, значения прогибов остаются неизменными. Сколько бы мы теперь ни продолжали расчет, значения прогибав останутся такими же. Процесс вычислений устойчив. Нарушен закон чередования знаков погрешностей - и неустойчивость процесса вычислений исчезает.

Мы говорим, что формула (1.16) должна давать точные зна-чеиия прогн1бав, а в нашем расчете они получились приближенными и отличаются от точных значений, наказанных на рис. 1.16 на 3-4 единицы младшего разряда. Может быть это свойство самих ите-рациоиных формул (1.18) и (1.19? Нет. Если они удовлетворяются, то будет удовлетворяться и формула (1.16).

Здесь мы имеем дело с погрешностями округления. В этом нетрудно убедиться, если цродолжить вычисления с большнм числом значащих цифр, но мы это сделаем в другом примере. А пака мы рассмотрим различные способы лостроения разностного уравнения и более сложный случай анализа устойчивости вычислительного процесса.

1.13. Разные разности

Мы говорили о том, что существует много способов построения разностных выражений, ашгроксимирующих дифференциальный оператор. Разностная формула в левой части уравнения (1.16) является самой простой формулой, аипрокшмирующей четвертую производную. Она будет единственной, аппроксимирующей четвертую производную на 5-точечном шаблоне. Но можно получить разностную формулу для шаблона, имеющего большее число точек.

На 7-точечном шаблоне можно получить бесконечное множество четвертых разностей, аппроксимирующих четвертую производную со вторым порядком. Запишем некоторые из них:

(- Ш+з + SWm+2 - 23Wm+i + Wm ~ 23ш , + (-Ши+з + 10а;;„+2 -31ш+, +44аУя2 -31ш,п 1 +

(1.20)

Покажем, как эти формулы получаются. Нужно обозначить коэффициенты при прогибах в семи узлах какими-то буквами, например а:, 02,.. ., аг, и представить четвертую разность в виде

(1.21)

Далее следует разложить это выражение в ряд Тейлора вблизи точки x=mh, сгруппировать одинаковые производные и приравнять коэффициенты при производных нулю, за иоключеннем коэффициента при четвертой производной, который должен быть равен единице. Если ограничиться в разложении только шестью членами, чтобы порядок аппрокоимации был вторым, то получается система из шести уравнений

«1 + «2 + «3 + 4 + 5 + «6 + 7 = О,

З/?! + 22 + - Дд - 2Дб - 3.<77 = о.

5 *6

9i?i + Аа + + 5 + + = О, 271 + Ва + «3 - й: - 8.7е - 27а, = О,

81t2i + 162 + 3 + 5 + + 81(7 = 96,

243.1 + 322

32ag - 243а7 = 0.

(1.22)

Считая одни из коэффициентов, например известным, можно выразить через него все остальные:

Й4=24-20й:1.

Теперь, давая коэффициенту йу различные значения, получаем разные выражения для четвертой разности. Любое из этих выражений аппроксимирует четвертую производную со вторым порядком.

А какое из этих выражений будет самым лучшим?

Это зависит от того, что мы намерены делать с ним дальше. Если, например, Т1ребуется получить лучшее приближение к четвертой производной, т. е. повысить гю1рядок а!Ппроксимации до четвертого, то к системе (1.22) нужно добавить еш.е одно уравнение

729ai4-64:2 + :3+a5+64a6-f 729й:7=0.

Это уравнение обраш.ает в нуль .коэффициент при шестой производной в разложении разности (1.21) в ряд Тейлора. Теперь коэффициент dl приобретает определенное значение: ai=-2/3. На 7-точечном шаблоне будет определена только одна разность, аппроксимирующая четвертую производную с четвертым порядком:

2т+з + 241Г-Ь2-781Г;+,+ . 15Л*

: + 112Г- 7SW., + 24W., -Шт-ь

Таким образом, можно строить различные разностные выражения, аппрокопмарующие производные. На 9-точечном шаблоне можно сконструировать четвертую разность, обладающую шестым поряд-

ком аппрокоимации, на И-точечном шаблоне - восьмым порядком и т. д.

Однако повышать порядок аппроксимации хорошо только до тех пор, HOiKa не ухудшаются другие качества разностной задачи. Замечено, что при большом числе точек шаблона вычислительный процесс может быть неустойчивым. Например, если в разностной формуле сохраняется чередозание знаков перед членами, то, естественно, начальные погрешности будут тем значительнее, чем больше число членов в разностной формуле н чем больше коэффициенты перед этими членами. В этом смысле наиболее интересна третья сверху фор.мула (1.20). В этой формуле самые маленькие коэффициенты и, кроме того, у нее необычное чередов1ание знаков перед членами. Знаки меняются по системе: один «--», два «-», один «--», два «-», один «--». Попробуем

решить нашу задачу о прогибах балки с помощью этой формулы. Приравняв нулю четвертую разность, получим разностный аналог дифференциального уравнения (1.13)

= 0. (1.23)

Нетрудно убедиться, что это разностное уравнение опять аппроксимирует дифференциальное уравнение с бесконечным порядком.

Решив уравнение (1.23) относительно прогиба в узле с номером т, получим итерационную формулу

+ 2П-2-П-з)/4.

(1.24)

Нас интересует устойчивость процесса вычислений с помощью этой формулы, поэтому не будем нарушать чередования знаков в оро-цессе вычислений, т. е. при вычислении следующего приближения учтем только прогибы, полученные в предыдущем приближении.

Теперь при вычгислениях будем использовать 7-точечный шаблон, пригодный для вычисления прогибов в узлах т с номером 3, 4, 5, 6, 7, и нужно подумать о том, что делать с узлами 2 и для которых формула (1.24) не годится, т. е. нужно -записать формулу для расчета прогибов в узлах 2 и 8.

Таким образом, при решении наитей задачи набирается несколько разностных формул для вычисления прогибов в различных узлах. Эти формулы определяют алго1ритм решения задачи на ЦВМ. Для записи алгоритма разработаны различные формы [2, 7]. которые в принципе мало чем отличаются друг от друга. Запись алгоритма по определенной формуле называется разностной схемой. Рассмотрим один из основных способов записи разностной схемы.

1.14. Разностная схема

Выше при решении задач мы так или иначе определяли способ вычисления искомых функций (давления, прогибов) зо всех узлах сетки. Прн этом многое объясняли словами. Такой способ формулировки алгоритма расчета не является строгим и иногда