Таблица f.J

Табтща 1Л уЗЛаХ МОДбЛИ В ПбрВОМ ПрИ-

ближении. Можно, например, в качестве первого приближения взять нули, что мы и сделаем.

Начнем вычисление значений Р во втором приближении с точки а. Для этого сложим имеющиеся значения давлений в соседних точках и разделим на четыре. В результате для точки а получим а(1)==:( 1,0+1,0-fO-f + 0) /4~0,5; проделаем ту же процедуру для точки b : ()=zz.(0,5+1,1 4-0 + 0)/4=0,4 и т. д.

Когда обойдем все точки области, получим второе приближение для значений давлений (табл. 1.2).

Теперь снова обойдем все точки области и вычислим давления по формуле (1.12), найдем второе приближение для значений давления. После нескольких таких обходов значения давлений меняться не будут (табл. 1.3). Следовательно, задача решена. В каждом узле удовлетворяется соотношение (1.12).

У читателя вряд ли хватит терпения довести эти вычисления до конца. Да это и не нужно. Достаточно подставить значения давления, взятые из табл. 1.3, в формулу (1Л2) и убедиться, что с точностью до 0,1 все они подходят для нашей формулы. Для наиболее упорных мы подскажем: чтобы быстрее достичь результата, нужно начинать расчет не с нулевых значений давлений во внутренних точках области, а с каких-то близких к истине, которые изменяют давление от лигиши; границы ДО границы плавно.

Рис. 1.14. Кроме того, рекомендуется не

ПЛОХО!

возвратно-поступательный обход точек, какой мы применили, а по спирали (рис. 1.14). При этих условиях мож- но получить решение, т. е. вычислить давление во всех. 36 точках за 4-5 обходов или, как говорят, за 4-5 итераций.

Вычисленные значения искомых функций позволяют вычислить все остальные величины, определяющие состояние среды. Это не сложно. В нашей задаче по полученным значениям давления можно найти: плотности; потоков, используя соответствующие разностные формулы.

1.11. Подводные камни

Оглядьшаясь «а решенную выше задачу, можно подумать, что все получается очень щросто. Нужно соста1Вить систему разностных уравнений, апороксимируюш/их исходную дифференциальную задачу, и решить эту систему, на1цр1имер, методом последовательных приближений. Однако на этом пути могут встретиться серьезные препятствия. Для примера рассмотрим еще одну характерную задачу,,, где рассмотренный способ последовательных приближений не :пр1И водит к решению.

Предположим, что балка, находящаяся на двух онорах (рис. ] .15), изогнута поворотам сечений на концах. Днфференци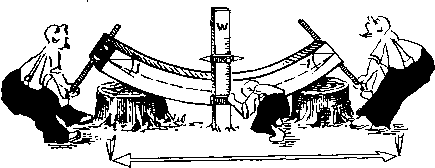

Рис. 1.15.

альное уравнение изогнутой оси балки в этом случае имеет вид

где w - гкрогиб балюи.

Эта задача является одномерной и стационарной и уравнение (1.13) можно решить точ-но, например, методом понижения порядка производных. Решение будет иметь вид

w=Cx + C2X+CiX + Co.

Постоянные интегрирования Со, С], граничных условий на концах балки:

(1.14)

и Сз определяются из

dw(0)

dw(l)

(1.15)

Производные от прогибов на концах балки взяты равными единице, т. е. угол наклона оси к горизонтали составляет 45°. Длину балки для простоты вычислений мы возьмем равной 1 м. Тогда, подставИв граничиые условия в уравление (1.14), получим значения постоянных Со=Сз=0, Ci=l, С2=-1 и точное ;решение будет иметь вид

w=x~x\ (1.16)

Это точное решение показано на «рис. 1.16. Там же дана таблица точных значений прогибов, вычисленных через 0,1 м по длине балки. Простые условия задачи позволили вьийсднть эти значения прогибов точно, т. е. полученные цифры ие содержат погрешностей округления.

Z? а2 0,и Ofi 0,8 10 X

0,1 0,2 0.3

Рис. 1.16.

/77-/

I Wrr.i-Wm-i \\ \\ Wm-m \\ Щ+г-тч\ Первые

I -h-II-h- и Ti I h 1 ровности

L ----JL - Jl---------1

1-;-2Щг}г-%,\I тг2т*;-Щ Вторые , ji \\ \ разности

I . 11 p 1 -j

1 \т.г3т3ш:г % j j Wfj,,z3w„j.f-3wwj Третьи I-P-ji V J разности

I Wrrj.rw.f6w-w~f%,\ Четвертая I--j-1 ровность

Рис. 1.17.

Теперь предположим, что мы не знаам точного решения и хотим вычислить его приближенно разностным методом. Для этого введем сетку с шагом Л=0,1 м:

(й = {х = т/г ( m = О, 1, 2, .... 10}.

Аппро.кслмлруем четвертую производную на этой сетке разностным выражением. Для этого выберем любые пять соседних узлов и запишем выражения для первых разностей между протибами в этих узлах (рис. 1.17). Получатся четыре первые разности, которые мы относи.м к центрам отрезков между узлами. Вычислим теперь разности от первых разностей, т. е. вторые разности. Их будет три, и они относятся к трем внутренним узлам (т-1), т и (m+l). Также вычисляются две третьи и одна четвертая разность. В результате получится вьгражение для четвертой разности на 5-точечном шаблоне

Погрешность от замены производной полученным разностным выражением пропорциональна h?-. Действительно,

dw 2h

дх"-

(2hY dw (2hY

dw (2hY dw (2hY

dx 4

dx h

/г* Удх 1! dw dw h

дх 4

3-421

дх 5! dw 2h

дх б!

h* \" dx 1! d*w {2hY dw

dx dw

"T" dx 2! (2hy dw

120/2

. dw

dw {2hy dx 3! (2hy \

500A*

dx* ax« 6!

0(Л2).

Таким образом, имеет место второй порядок аппроксимяции производной четвертой разностью. У!ра1внен1ие (1.13) заменим теперь разностным уравнением

- Jji =и. (1.16)

А каков будет порядок аппрокси-мации дифферендиального уравнения (1.13) разностным уравнением (1.16)? Если учесть, что из уравнения (1.13) следует

dx Тх" • •

то порядок аппроксимации получается бесконечным. Это значит, что формула (1.16) должна привести к точным значениям прогибов в узлах сетки.

Теперь нужно аппроксимировать также граничные условия (1.15). Для этого производные от прогибов по координате в граничных узлах заменим разностями

dw(0)

Wj - Wq fdw(l)

Поскольку шо=£У1о=-0, получаем йУ1=0,10 и и;9=0,10.

Таким 01бразом, для задания граничных условий в крайних узлах прогибы нужно положить равными нулю, а в соседних с крайними-0,10. Но чтобы не вносить в (расчет погрешности со стороны Граничных условий, мы в соседних с крайними узлах сетки будем записывать точные значения прогибов, т. е. 0,09. Нам останется вычислить методом последовательных приближений значения прогибов в семи внутренних узлах сетки.

Итерационную формулу, как и ранее, получим, решив уравнение (1.16) относительно прогиба в центральном узле ш:

i+\ -

<+2 + 4

+ 4< ,-< 2)/6,

(1.17)

где i - номер приближения.

Теперь нужно договориться о значениях w в первом приближении. Если взять в качестве первого приближения точные значения из таблиды на рис. 1.20, то с помощью формулы (1.17) полу-Чгим тачные значения, например, для центрального узла (т=5):

0.21 + 4.0,24 +4.0,24 - 0,21

= 0,25.

Это подтверждает наш вывод о том, что уравнение (1.16) обладает бесканечиым порядком аппрокоимацни.

Но если точные значения щрогибов неизвестны, то в качестве первого приближения можно взять любые числа. Мы же возьмем числа, близкие к точным, чтобы иметь возможность оценивать погрешности при каждом следующем приближении. Начальную погрешность в первом приближении примем меньшей 0,05. Для этого просто округлим точные значения до 0,05.

Числа первого приближения (i=i) приведены в первой строке табл. 1.4. Далее в таблице идут результаты вычислений с помощью

Таблица 1,4

итерационной формулы (1.17) следующих приближений, вплоть до десятого.

Оказывается, что погрешности с каждьгм приближением не только не уменьшаются, но быстро растут и на десятом приближении превышают 0,5, т. е. составляют 200% ог точных значений прогиб оз в центре балки.

Интерадионный процесс оказался неустойчивым,

1.12. Устойчивость

Постараемся ответить на опросы: что такое неустойчивость вычислительного процесса? В чем причины пеусгончивости? Обратим внимание на то, что при подстановке в формулу (1.17) точных значений nporHi6oiB в следующем приближении получаются также точные значения. Но если в начальных значениях появляются погрешности, то они возрастают. В данном случае имеет место определенный вид неустойчивости: неустойчивость вычислительного процесса по начальным данным.

Таким абразам, неустойчивость по начальным данным - это быстрое возрастание начальных погрешностей.

Ответ на первый из поставленных вопросов вызывает еще два вопроса: какие кменно начальные погрешности увеличиваются при неустойчивости?

Что значит: «быстрое нарастание погрешностей?»

Оказывается, при неустойчивости по начальным данным увеличиваются не все полрешности, а только те из них, графики ко-торых имеют вполне определенный вид. В данном случае усилива-