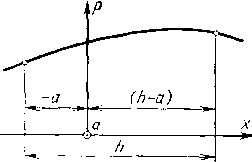Рис. 1.13.

порядком аппроксимации. Порядок аппроксимации показывает, каким образом снижаются погрешности с уменьшением шагов сетки. Если, предположим, порядок аппроксимации первый, то погрешности пропорциональны шагу, если второй, то - квадрату шага и т. д. Покажем, как определить порядок аппроксимации на примере замены первой производной первой конечной разностью. Допустим, мы хотим заменить производную в точке О (рис. 1.13) и для этого наметили два узла сетки в точках x=-а и x=h-а.

Будем считать функцию Р и ее производные в точке О известными. Воспользовавшись разложением этой функции в ряд Тейлора, находим значения функции на концах отрезка при х=-а и x=h-а:

дР а , дР дР . дР

Р(- =

P{h - a) = P

дх, 1!

дР (Л дх

дх 31

дх* 4!

дх 21

дР (h~ay 1 дР (h-aY дх

Теперь можно определить значение*конечной разности

Р (h~a)~P(--a) дР . дР h - 2a дР h-~3ah + 3a

дх д-с 21

\д*Р - Aha 4- Qha 43 дх* 4!

(1.6)

Погрешность от замены первой производной конечной разностью будет равна

P(h-a)-P(~-a) h

дР дР h~2a

дх 3ha + 32

ду,*

Если величине а давать различные значения от нуля до А1, то получатся различные значения погрешности При

ki=0 разность (1.6) будет правой разностью и погреш-I ность будет равна дР h \ дР

дх~ 2! дх 3!

Она ,пол}чается пропорциональной шагу сетки. Имеет место первый порядок аппроксимации производной «правой» разностью. Условно это в принятых выше обозначениях можно записать в виде

Рт+г.п-Р,п.п дР , Q

h дх

Производная вычисляется в узле на левом конце отрезка mhx-(m~\~\)h. Уравнение (1.7) читают так: разность равна производной плюс остаток, пропорциональный h.

К аналогичному результату мы придем при а=/г. В этом случае разность (1.6) будет «левой» и погрешность составит дР h , дР h}

дх~ 21 дх 3!

Знаки производных, которые получаются в результате решения, нам заранее неизвестны, поэтому нельзя сказать, будет ли эта погрешность больше или меньше, чем для «правой» разности, но в обоих случаях она будет пропорциональна h. Для левой разности можно записать

Рт,п-Ргп-г,п дР , Q

Если же взять a=hf2, то погрешность уменьшится и будет пропорциональна квадрату шага h:

4}*Р \Р

4-3 ! dxJ 8"+" •

Таким образом, заменяя конечными разностями произ-Юдные в узлах сетки, получаем первый порядок аппроксимации, а в центре отрезков между узлами - вто-1ЮЙ [7]:

т+1,п

0,5/1-f О (Л).

(1.9)

Теперь можно ответить на вопрос: как располагать ¥злы сетки, чтобы поточнее вычислить производную спо-10ш.ью первой разности?

Для вычисления производной в какой-то точке х, узлы сетки следует располагать на равном расстоянии

по обе стороны от точки л:, т. е. в точках x+hj2, х-hj2.. А если нужно вычислить с помощью разности первую производную в точке, где уже имеется узел? В этом случае лучше воспользоваться «центральной» разностью

Pin+i,n Рт-\,п Р

(1.10)

водной в узле второй разностью должен сохраниться вторым.

проверим это. , Используя разложение функции Р в ряд Тейлора иблизи точки x=mh, получаем

Порядок аппроксимации в этом случае будет вторым, а не первым, как в случае «левой» и «правой» разностей.

Это правило хорошо согласуется с физическими представлениями. Например, если давление в нашей задаче о течении жидкости вычисляется в узлах сетки, то разность давлений и соответствующая ей производная пс координате определяют поток между узлами и относятся к центру отрезка между узлами.

Мы говорили об аппроксимации производных конечными разностями. Можно говорить об аппроксимацик всего дифференциального уравнения конечно-разностным уравнением и, наконец, об аппроксимации всей дифференциальной задачи конечно-разностной задачей. В любом Случае можно определить порядок аппроксимации

Аппроксимация определяет только погрешность от замены производной или дифференциального уравнение конечно-разностным выражением. Если, например, .скорость точки мы вычисляем как первую разность от перемещений по времени при известном значении пе ремещений, то величина ошибки равна погрешность вычисления скорости. Если же решение задачи нам не известно, то аппроксимация говорит лишь о том, чт( решение системы разностных уравнений будет похожие на точное решение, что уменьшение шагов сетки при водит к уменьшению погрешностей и что порядок по грешностей определяется порядком аппроксимации.

Рассматривая теперь производную dPjdx как неко торую функцию координаты х, замечаем, что при стрем лении шага сетки h к нулю вторая разность стремится: к производной от производной, т. е. ко второй произ водной:

Рт + 1,п ~ Рщ.п ~ Рт~1,п Р .

lim------

Вторая производная опять определяется в центре интервала {т-0,5)/i ... (/п + 0,5)Л, на концах которогс были найдены первые разности, т. е. в узле сетки т, п Следовательно, порядок аппроксимации второй произ-

2! h

дх дР

гп,п гр

Р ) к \дР

дР h

-2Р-\-Р

дР /г*

О(Л).

Действительно, имеет место второй порядок аппрок •1Имации.

Теперь можно сказать, что для улучшения аппрокси-!\1ации все четные производные следует определять \\ узлах сетки, а нечетные - между узлами. Нуль считается четным числом, а нулевая производная будет самой функцией Р.

Если теперь совершить в уравнении (1.2) предельный переход от разностей к производным и по координате у, 10 уравнение можно записать в таком компактном виде:

(1.11)

Мы получили известное уравнение в частных производных- двухмерное уравнение Лапласа. Этим уравне-ЧИем описываются не только процессы в жидкостях, но И стационарные тепловые процессы в твердых телах, процессы фильтрации и многие другие. Разумеется, II процессах другой физической природы нужно взять иМесто давления какую-то другую физическую величину, например в тепловых - температуру, в электрических- потенциал и т. д. Да и в нашем процессе течения жидкости давление можно принять в качестве искомой функции только в случае горизонтальных потоков жидкости 1большой высоты. Если нашу модель с водой распо-лЬжить вертикально, давление Р в качестве искомой <(ункции брать нельзя. Действительно, мы знаем, что Авление в нижних слоях воды выше, чем в верхних, это не значит, что вода всегда течет снизу вверх.

1-8. Что может высшая математика?

Уравнение Лапласа записано нами для произвольной j точки области и годится для любой точки, где протека-ют потоки воды. Если заданы граничные условия на краях рассматриваемой области, то можно в принципе проинтегрировать полученное уравнение по области и получить точное решение задачи. К сожалению, в практических задачах вряд ли это возможно. Давайте подумаем что значит найти точное аналитическое решение задачи Это значит найти такое аналитическое выражение функции Р, которое в каждой точке области удовлетворяет уравнению Лапласа, а на границе принимает заданньк значения. Это аналитическое выражение должно быть составлено из хорошо изученных элементарных функций: тригонометрических, гиперболических или степенных Заметим, что все эти функции сами являются решениям;; дифференциальных уравнений, но более простых, одномерных, и чаще всего бывает так, что из них не удаетс; * скомбинировать решение двухмерной задачи.

Общих методов интегрирования дифференциальньп уравнений нет. Недаром математики говорят не «решит! задачу», а «отыскать функцию, удовлетворяющук: уравнению», т. е. решение надо искать. А найдешь иля не найдешь - еще неизвестно. Каждое найденное аналн тическое решение дифференциального уравнения в мате матике - целое событие. Значит, аналитические решение попадаются редко. Как же быть?

1-9. Назад - к конечным разностям

Выход есть. Если задачу нельзя решить аналитиче скими методами, то ее, как правило, решают численными методами, например методом конечных разностей В рассмотренном выше примере нужно решать не диф ференциальное уравнение Лапласа, а разностное (1.2j.

Разностное решение всегда приближенно, но точност! его тем выше, чем меньше шаг /г. С другой стороны, нам точные решения и не нужны. В большинстве случаев до статочна точность в один, максимум два десятичных зна ка. Более того, точных решений принципиально лолучип f нельзя, даже если решим дифференциальное уравнение так как мы не знаем точных значений величин, входя щих в условия задачи. Нам достоверно не известны раз

меры деталей конструкции, характеристики материалов, внешние воздействия на конструкцию. Поэтому погрешности расчета нас не должны смущать. Да и сами дифференциальные уравнения не точно отражают физическую картину явлений. В частности, при их выводе используется гипотеза о линейности среды, а реальные среды, как известно, нелинейны.

1.10. Как решать?

Теперь постараемся ответить на вопрос: как решать задачу разностным методом? Вернемся к примеру с водой. Предположим, что нам заданы давления в граничных резервуарах или в граничных точках нашего поля. Дадим им численные значения из условий задачи, например такие, как в табл. 1.1.

Постараемся найти значения давлений во внутренних точках области. Эти значения должны удовлетворять уравнению 1. Запишем его в более простом виде, сократив на /г и перенесем Рт,п в правую часть:

т,п-{-\

* т,п- 1/

(1.12)

Полученное уравнение говорит о том, что давление в каждой точке должно быть равно Среднему арифметическому давлений в четырех соседних точках. Если удастся вычислить давления в каждой точке, удовлетворяющие этому условию, значит, задача будет решена.

Можно решать задачу так. Обозначив давление буквами а, 6, с, ..., составить 36 уравнений (1.12) и решить их относительно 36 неизвестных давлений. Но решать систему из тридцати шести уравнений с тридцатью шестью неизвестными «на руках», не используя ЭЦВМ, прямыми методами (методом Эйлера или Гаусса) сложно. Поэтому мы применим другой, более простой и в данном случае более экономичный метод последовательных приближений.

Заполним все клетки таблицы числами, т. е. определим значения Р во всех