ют одинаковые размеры, Эти элементы можно назвать элементами массы (рис, 3.33). По боковым граням элемента массы со стороны «соседних элементов дснста\тот нормальные и касательные напряжения. Нам неизвестен закон распределения этих напряжений по плоскости грани, но мы можем суммарное действие каждого вида напряжений заменить равнодействующей силой.

Нам потребуется одно уравнение движения, -которое получается, если спроектировать равнодействующие на иаправленне вертикальной оси г.

Отличными от нуля получаются только проекднн на вертикаль равнодействующих касательных напряженпй

°г ~z.: -Оэзиачим ЭТИ проскцип символами

Q{x-\-hi2), Q(xhl2), Qiyhl2) и Q(y~h!2) соответ-ствеиио, тогда уравнение динамического равновес1[я можно будет записать в виде

С(л- + Л/2)-Qfx-/i/2)Q(i/ + .;/2) -

-Q{y-h!2)=nia,, (3,32)

где т --Масса элемента.

Равнодействующие, деленные на обтаем элемента массы, обычно называют перерезывающими силами. Для определения равнодействующих выделим для каждого элемента массы четыре элемента, которые назовем элементами перерезывающих сил (рис. 3.34). Элементы перерезывающих сил смешены относительно элемента массы на половину шага и наложены один иа другой.

Рассмотрим отдельно элемент для определения равнодействующей Q(jt-b0,5) (рис. 3.35), она приложена посредине нового элемента, Но напряжения можно считать EHernHnMH по отношению к элементу только в том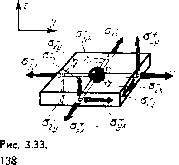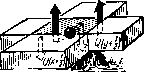

Р-ис. 3.34.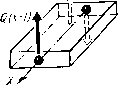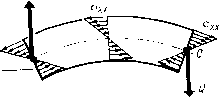

Рис, 3,35.

Рис. 3,36.

случае, если отб!рошена часть области по сечению, где указаны напряжения. Поэтому приложим две новые равнодействующие Q(a-[-1) н Q по граням нового элемента и будем считать, что равподействуюи1,ая Q(,\--rO,5) равна среднему арифметическому новых равнодействующих:

Q(.v + 0,5) = [0(x+l)-Q]/2.

Составим уравнение равновесия нового элемента. Поскольку равнодействующие образуют момент сил, то уравновесить их можно толшо с помощью другого момента или нескольких моментов сил. Такими моментами, (пр11Ложе]шьшн к элементу парерсзывагощих сил, будут моменты нормальных и касательных напряжений и сРд-у (рис. 3,36). При изгибе пластины вверх верхние слои будут растягиваться, а нижние - сжиматься, поэтому выше срединной ловйрхности напряжения будут направлены ог дентра пластины, а ниже - к центру. Таким образом, напряжения будут создавать моменты. Чтобы вычислить величину момента, внзчсле вычисляют величину нормальных напряжений в зависимости ог удаления слоя от срединной поверхности. Для этого нам и послужит гипотеза прямых нормалей.

Запишем новое выражение дтя нормальных напряжений через деформации растяжения. Прежние выражения (3.5) теперь непригодны, так как из трех деформаций растяжения, входящих в каждое уравнение, можем определить только две, лежащие в плоскости пластины и оаредслиемые с помощью гипотезы прямых нормалей. О дефор-мацин в направлении нормали к плоскости пластины мы ничего сказать не можем. Яеней вопрос с напряжениями. Если на пластину не действуют внешние силы, нормальные к поверхности, или такие силы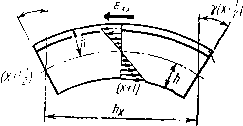

Рис. 3.37.

Приложены с одной стороны, то можно считать, -что напряжения cTjz по всей толщине отсутствуют. А для двух оставшихся нормальных напряжений можно по аналогии с уравнениями (3.3) записать

В У»

Решив эту систему относительно нсиз;вестных напряжений, получим

В полученные выражения, естественно, не входит относительное удлинение в направлении г. Нам нужно только первое из этих уравиеиий.

Теперь исходя из гипотезы прямых нормалей определим деформации Zxx н гуу в нужных сечениях. Эти деформации зэЕнсят от удаления слоя, для которого они вычисляются, от поверхности пластины. Возьмем слой, находящийся на самой поверхности (рис. 3.37). Нужно определить деформапии ev в точках х и (д: + П. Для этого выделим повые эле.менты, которые можно назвать элементами изгибающих моментов. Для определения деформаций растяжения нам потребуется восемь таких элементов, из которы.х четыре совпадут с элементом массы.

Абсолютное удичинение у поверхности нового элемента выражается через углы поворота сечений. Если за положительное направление отсчета углов принять направление против часовой стрелки (см. рис. 3.37), то абсолютное удлинение составит k{y (д:-Ь 1,5)-у("Ь0,5)], а оиоснтельное будет в раз меньше:

e,,(A--f-l) = A[Y(A-bU5)-~Y(4-0.5)P,. (3.33)

уц) Еда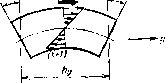

Рис, 3.38,

Рис. 3.39.

Теперь нужно определить относительное удлинение в той же TOHiKe (л:4-1), ио в направлеиин норма.чи к плоскости чертежа (ом. рис. 3.37). Для этого рассмотрим изгиб тех же элементов изгибающих моментов в .плоскости yOz (рис. 3.38). Относительное удлинение в направлении у будет у поверхности определяться выражением

tyy{x\)=h[<{x-\-\, y~i),b)-{x~\, i+0,5)] T,,.

Подставив полученные зиачеиня относительных удлинении в первое выражение для нормальных иа[1ряже-н][й, получим

Eh ff (+.5)--Y(x + 0.5) А.

(3.34)

Относительные удлинения согласно гипотезе прямых нормалей распределены [Ю сечению ло линейному закону, поэтому также будут распределены и напряжения ахх (рис. 3.39). Это позволяет легко рассчитать изгибающий ;момеит В сечении. Заменим ]1апряжсния двумя равнодействующими (для Bcp\jj4*ro и нижнего треугольника). Они будут равны площадр! треугольников, образованных диаграммой напряжений, умиожеизюй на ширину элелтента hy-.

РхР=0,5<Тхх(>:+1)/Ау,

Эти равнодействующие будут приложеп!ч в центре треугольников, т, е. иа расстоянии 21/3 от срединной поверхности. Поэтому создаваемый ими момент Му{х-\г\) =

4P/t/3=2ft=*V«(+ 1) /3.

Подставив сюда значение нормальных напряжений (3.34), получим выражение изгибающего момента через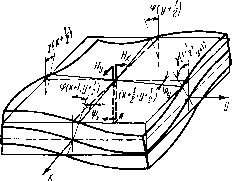

Рис. 3.40.

углы поворота сечений:

1 - у=

1,51-Y (1С+ 0,5)

(3.34а)

Касательные наоряжения возникают на боковых поверхностях элемента перерезывающих сил вследствие закручивания пластины (в виде пропеллера). Они образуют моменты сил, которые называют крутящими. Для их нахождения выделяют четыре элемента (рис. 3.40). С помощью каждого такого элемента определяют два крутящих момента в двух взаимно перпендикулярных вертикальных плоокостях.

Касательные наотряження, действующие по граням с нормалями X и у, определяются одной и той же суммой углов -ух п у. Вблизи поверхности элемента касательные напряжения

2(l+v)

Нормальные напряжения определялись через модуль Юнга и коэффициент Пуассона, поэтому касательные на-гьряжения выражены ие через модуль сдвига а через модуль Юнга и коэффициент Пуассона.

Углы [зх н -фу на поверхности пластины следует определять через углы поворота сечений, например:

ф,ЛНср(х+1; j/ + 0,5)+9(£ + 0,5)l/V % =h [т(- + 0,5; I) - у(л- + 0,5)]М,.

Крутящие моменты, создаваемые касательными напряжениями, вычисляются та.к же, как и изгибающие моменты:

:Я,(л-+0.5; ,+0,5) = !-.ii X

3 3(1+V)

lY (-+0,5; у+1)--г (х+0.5) ч>(х+ 1; f/+ 0.5} - у (iy + 0,5)

(3.35)

Я,(. + 0,5; i/ + 0.5) = -2AV.x(-v-hO,5; у + 0,5)/3.

Напомним, что моменты считаются положительными, если они вызывают вращение против часовой стрелки, поэтому положительные касательные напряжения а,; создают отрицательный момент Ял-.

Р«с. 3.41.

Теперь, когда определены все изгибающие и крутя-щие моменты через углы ттоворота сечений, можно приступить iK вычислению неререзываюи;их сил. Для этого вернемся К равновесию элемента перерезывающих сил (рис, 3.41).

Проектируя моменты на ось г/, получаем;

IQ (X + 1) А, -L Q/iJ/2(л:-h I) + , (х -Ь0.5; £ + 0,5)- ,(. + 0,5; у-0,5).

Учитывая, что псререзыиающ;я сила, приложенная к элементу массы, равна полусумме перерезывающих сил Q и Q(jt:+l), мож1[о записать

Q(x+l) = l.M,(.v-l)-/M,,-f ,(,.--1-0,5, -! 0,5)4-

+ (x-hO,5, t/-0,5). (3.36)

Теперь остается только iHiipa:(HTb углы поворота сечений через перемещения узлов модели-сотки в вертикальном направлении, или, что то яе слмос, iKpcj njio-гибы пластины. в вьгряжсния тести изгибающих моментов входит 24 угла поворота. 7Хля и\ определения выделяется 24 элемента углов поворота сечений (рис. 3.42),