+х гг

- £ - - т)] 4-

-с - )]=-ь 2++2) +

Если теперь ввести обозначение для отношения эффипие[[тов упругости к коэффициентам вязкости то в силу равенства (3,30) этот (коэффициент будет универсальным:

л----х "1 Л+2[1.

И можно ИСКЛЮЧИТЬ прежние коэффициенты потерь с и т) и оставить один коэффициент Л. Тогда сумма упругих и б>]зких напряжении перепишется в виде

+ <хх [( 4- 2f.) с 4- я; ь-1 -

- л, [(Я -ь 2fi) <; ( - X) я.;; ( - х)+я.;; ( - )=

(l l4 -Л а-(-х).

Таки1 образом, с помощью нового коэффициента удалось выразить сумму ynpys их и вязких напряжений через один упругие напряжения, вычисленные в два последующих момента времени {i-t) и i. Проделав ту же операцию со всеми напряжениями в выражениях (3.6), можно получить уравнения движения в виде

(1+Л)и-Ли(-х)=ра„

(>+,)У + ЛУ(-х)==рй,,

(l+Л)W-ЛW(-•=) = pa,,

где большими буквами U, V и W обозначены выражении, соответствующие левым частям уравнений равновесия (3,6), вычисленные в два woMeHTa времени.

Величины и, V и W при расчетах по формулам, где вязкость не \иты.вается, вычисляются в каждом шаге по времени, поэтому при расчетах по формулам с учетом вязкости их не надо вычислять два раза. Доста-132

точно запомнить выражение, получившееся в предыдущем шаге вычислений, и использовать его в последующем шаге.

Теперь МОЖНО записать уравнения (3.13), для которых мы будем составлять программы вычислений с тем, чтобы в этих уравнениях учитывалась вязкость. Введем обозначения, удобные для программирования на языке ФОРТРАН:

т = щ1-х\ D4 = -n,

D5 = -V, D6=-

Л1 = 1 + А, А2Л.

Уравнение (3.13) запишется в виде

из Л1 %D4 - A2>tcD 1 4-2>tcU2 - и 1.

V3==A1D5-A2;4cD2 4-24:V2- VI,

W3 = AlD6 - A2>tcD34- 2\V2 - W1,

D4 = QXX1 - QXX2 4-QXY1 - QXY2,4-QXZ1 - QXZ2, D5 = QYY1 - QYY2+ QYZI - QYZ24-QYX1 - QYX2» D6 = 0ZZ1 - QZZ2-i-QZXl - QZX2QZYl - QZY2.

Теперь расскажем о том, как определить числовое значение коэффициента Л. В выражение этого коэффициента Л=:т],т входит коэффициент динамической вязкости

твердого материала г). В спрат50чной литературе числовых значений >- не встречается, но можно выразить т) через логарифмический декремент затухания у, который можно получить экспериментмльно, а его значения для разных материалов можно найти в справочниках.

Выражен11е i через у получается npii точном решвшш простых урааноннй: колебание струны, ггродольн1/с [(олобания стэрж]1я или плас-ТИЕ[ы. -Можно, напри-мер, 1вос110.1гьзОНа:ься ;реше:знем задач о колебаниях стержня и пластины, приведенными в книге Л. Д. Ландау и Е. М. Лифшица «Теория упругости», где приводится выражение для коэффициента затухания холебааанй 5. Этн выражения довольно гр,0МОздкн, но если перейти к лаилин обозначениям, учесть гипотезу (3.29) 1и то, что коэффВДиент внякости 1, равен £--2/3П, то вьйражения для чрезвычайно упрощаются н получаются в задачах ;для стержня и лластины одшналоными: р=ю*т(/2и.. Учитывая, что у=2л5/ш, лепко лолучить [выражен:]я для нашего кпчффиццснта

вязкоста r=Vfi/n». Учитывая, что laeroxa колебаи-ип oj, как правило, заранее шзестла, оычжлить коэффиаленг вязгпсли не лред-стазляет т"э\яа.

3.12, Подготовка исходных данных

Подготовка задачи для решения ее иа ЦВМ состоит из двух частей: подготовки исходных данных и программирования.

На вопросах программирования задач при цифровом моделировании механических и тепловых процессов в радиоконструкциях мы останавливаться не будем. Ограни-чимся только записью формул иа алгоритмическом язы1ке ФОРТРАН, поокольку эта запись мало чем отличается от записи обычных алгебраических вьграже-ний в принятой нами системе обозначений.

Если 1П]ри постановке задач па ЦВМ программирование может быть поручено специалистам по программированию, то подготовка исходных данных задачи должна быть выполнена самим конструктором. К таким исходным данным относятся в первую очередь коэффициенты, которые используются в уравнениях движения.

В случае неоднородного блока таких коэффициентов получается довольно много. К Каждому элементу массы мы отнесли 9 элементов связей для вы-числения нормальных напряжений и 12 для вычисления касательных напряжений. Для каждого элемента связи вычисляется свой коэффициент. Один коэффициент должен уштывать среднее значение плотности, а другой (А) -отношение сил вязкости к силам упругости. Таким образом, для каждого элемента массы нужно вычислить 23 шэффи-циента. Если в модели 1000 узлов, то получается 23 000 >коэффициенто1в.

Вычисление коэффициентов вручную занимает много времени. У опытного расчетчика такая работа отнимет около месяца. А поскольку эта работа однообразна и утомительна, то нужно еще примерно столько же времени, чтобы обнаружить сделанные им ошибки. Поэтому при подготовке задачи предстйвляет интерес машинное вычисление коэффициентов. Основные идеи состав-леиня программы для такой операции состоят в следующем:

1) Задаются размерами блока, что особенно просто, есчи он имеет прямоугольную форму.

2) Задают шаги сетки в направлепин всех трех координат.

3) Составляют таблицу всех однородных областей. Границы обласгей можно задать в виде коэффициентов в уравнениях наружных поверхностей области. В радио-конструкциях, как правило, можно выделить два типа областей; прямоугольные .параллелепипеды с гранями, параллельными координатным .плоскостям, и цилиндры, ориентированные по направлению одной из координатных осей. В таблицу заносят для каждой области значения модуля Юнга, коэффициента Пуассона, плотности и отношение Л, наполнитель в таблице не указывают.

4) В процессе расчета коэффициентов для каждого узла вначале вычисляют его координаты.

5) Проверкой всех областей устанавливают принадлежность узла iK одной из областей. Если узел не попадает ни в одну из областей таблицы, значит, ои относится к области наполнителя.

6) Проверяют наличие границ раздела между материалами на расстоянии шага от узла. По этим расстояниям вычисляют относительные объемы аг и относительные длины

7) По формулам для осреднсиных значений хара.кте-ристик вычисляют средние значения коэффициентов.

Алгоритмизация и прорраммирование такой задачи затруднительное дело, но зато однажды составленная программа может служить для вычисления коэффициентов при расчетах любых блоков.

Другая трудность состоит в том, что для хранения всех коэффициентов потребуется довольно большой объем оперативной памяти. А как мы указывали выше, применение внешних запоминающих устройств реко увеличивает время вычислений. Поэтому представляет большой интерес при расчетах неоднородных блоков р;:зличное упрощение модели.

3.13. Упрощение задачи

Упрощение задачи всегда основывается на особенностях коиструкцЕ1Й, поэтому в .каждом .конкретном сл\!ае нужно нс,"-;ать такие особенностн.

Мы остановимся на упрощенных, которые можно ввести в модель двух типов монолитных блоков, встречающихся в практике конструирования радиоаппаратуры.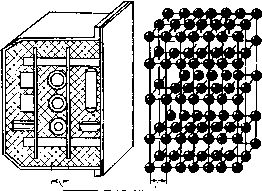

Рис. 3.32.

К первому типу относятся блоки, где механическую нагрузку несут в основном платы с радиоэлементами, и платы располагаются в виде «слоеного пирога» (рис. 3.32). Если прн построении модели такой коистрк-ции расположить узлы сетки с тем же периодом, что и расстояние .между платами, или взять расстояние между узлами в два раза меньшим, то число различных типов элементов связи резко сокращается. Их можно разбить на несколько групп и соответственно вычислить несколько групп коэффициентов. Прн составлении программы для каждого узла нужно будет только указать признак, некоторому следует выбирать коэффициенты.

Часто встречаются также конструкции блоков, где механическую нагрузку несет сам на1Ю.?нитель. Если наполннтеле?л служит компаунд, и его механические свойства мало отличаются от механических свойств плат. Такой блок в первом приближении является однородным, и все коэффипиенты упругости и потерь иа внутреннее трение можно считать одинаковыми. Йсжлючеиие составляет осредненное значение плотности. Плотность металлических деталей, являющихся частью радиоэлементов, можно учесть в расчете иведеинем одного для каждого узла коэффициента.

Можно использовать для упрощения модели идеи построения двухмерных моделей для расчета плоских и коробчатых деталей, которые излагаются ниже.

3.14, Модели плоских и коробчатых конструкций

Мы уже встречались со случаем областей прямоугольной формы (см. гл. 2), когда один из размеров области значительно меньше двух других. К таким областям относились тепловые экраны, кожуха и другие детали. Для иих мы строили двухмерные модели-сетки и исключали из расчетных соотношении одну из координат.

При расчетах процессов вибраций плоские и коробчатые детали играют особую роль. Поперечные или изгибиые !колебания таких деталей в радиоконструкциях наиболее опасны, поскольку амплитуда колебаний у них, как правило, значительно больше, чем в м01юлитных блоках. Радиоэлементы, смонтнроваиные непосредствеи-ио на плоских деталях, например платах или шасси, воспринимают полиостью эти колебания.

При построении моделей для расчетов процессов теплопроводности в пластинах исключение одной координаты производилось иа основе предположения, что температура по толщине пластины изменяется по лииейссому закону. Такое допущение можно использовать и при построении моделей для расчетов вибраций.

3.15. Гипотеза прямых нормалей

Эта гипотеза говорит о том, что все прямые, нормальные к срединной плоскости пластины до деформирования остаются прямыми и нормальными к иен после деформирования. Сама срединная поверк[Юст1-. искривляется, но ие испытывает растяжения. Гипотеза прямых нормалей позволяет построить для пластин двухмепчые модели, в которых узлы располагаются в одной плоскости. Кроме того, S расчетных соотношепнях для пл;!::тик остается одна переменная - перемещение в н:п1равле-нии нормали к пластине (прогиб), что значительно упрощает расчет.

3.16. Уравнение изгибных колебаний

Для составления уравнения движения пластины разобьем ее на элементы прямоугольной формы. Рассмотрим случай регулярной сетки, когда все элементы име-