Выисление p.

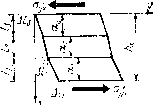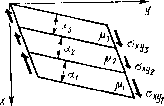Рис. 3.27.

Рис. 3.28.

экспериментов, к ка.ким мы прибегли при определении среднего значения модули Юнга.

Предположим, что к неоднородному элементу связи приложены касательные напряжения в плоскостях, параллельных границам раздела между материалами (рис. 3.27).

Так как касательные напряжения в любом сечении, параллельном границам, одинаковы, деформации сдвига каждой части элемента можно вьгчислить по формуле для однородного материала:

Сдвиг каждой части вследствие такой деформации пропорционален толщине этой части: SU=?.yxxU- Полный

сдвиг будет равен сумме частных сдвигов /=2

сдвига - отношению сдвига

а полная деформация к тачщиие элемента:

h

II,. (3.28)

Сравнивая полученное выражение с (3.27), получаем среднее значение модуля сдвига

Если касательные напряжения приложены по нормали К границам раздела (рис. 3.28), то, чтобы деформации сдвига частей элемента были одинаковыми, каса тельные напряжения, приложенные к каждой части, должны быть различны:

Равнодействующая касательных напряжений, приложенная к каждой части, определяется произведением i-Oxyiihz. Средняя величина касательных напряжений (авна отношению суммы равнодействующих к площади рани:

V.F,

среднее значение модуля сдвига при вычислеиип каса-гельиых напряжений можно найти по формуле

Теперь мы имеем полный набор формул для зычисле-[ия средних значений .коэффициентов Ламе для грании )аздела, параллельных граням элемента связи. Если )аницы сложные, полученные формулы можно применять последовательно к частям элемента связи. Пусть гемент связи имеет сложные границы раздела между Отдельными материалами (рис. 3.29). Криволинейные рверхности в таком элементе заменяем плоскостями, параллельными граням. Разумеется, используя конечное [исло плоскостей, можно произвести такую замену )лько приближенно. Разрежем наш элемент на части faK, чтобы в каждой остались границы, параллельные дной грани (рис. 3.30).

С помощью полученных формул осредним механиче-jKHe свойства каждой части, т. е. заменим неодиородные lacTH однородными. Затем сложим части в более круп-ib[e куски, но так, чтобы остались границы раздела, па-(аллельные одной праии, и снова проведем осреднение.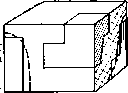

3.29,

Рис. 3.30.

После повторения этой операции несколько раз получим осредненныс характеристтжи .всего элемента связи.

В связи с введением операции осред-нення возникает вопрос: а нельзя ли осреднить весь блок и вместо [[еод-иородного блока получить однородный? По-видимому, можно. При расчетах вибраций такого осредненного блока пол\им средние характеристики движения. Но что будут означать эти характеристики - сказать трудно. Во всяком случае, при каждом осреднении мы доп>Ска-ем целый ряд погрешностей. Например, при рассмогре-нии р.ис. Я.2Г) и 3.26 НС уччтывались краевые эффекты. Вследствие этих эффектов границы раздела между материалами будут искривляться.

Вследствие искривления напряжения нельзя считать одинаковыми в каждом сечеинн. Будет происходить концентрация напряжений в отдельных местах. Начинает сказываться взаимодействие с соседними элементами. Ничего этого мы не учитывали и допускали появление погрешностей. Чем меньше размеры элементов связей, тем меньше и погрешности. Поэтому размеры приходится выбирать минимально допустимыми исходя из возможностей современных вычислительных машин. И следует заметить, что точность расчета неоднородных областей цол\ается значительно менее высокой, чем однородных. Но ничего более под.ходящего для расчета вибраций нсод]1ородных блоков РЭА еще пока не придумали.

3.11. Потери энергии на внутреннее трение

До сих пор мы рассматривали только одну сторону liponeccoB деформирования упругих тел, а именно упругие деформации. Но процесс деформирования всегда сопровождается потерями энергии на внутреннее трение в материалах конструкции. Это другая сторона процессов дефоршгрования. В металлических материалах эти потери невелики, и в большинстве случаев их можно не учитывать. Но при рассмотрении моделей неодно[родньг\ блоков РЭА приходится вводить эти потерн в модель. Ведь многие материалы, и в первую очередь наполнитель, б.водягся в блок специально для гашения вибраций п иМеют большие потери на внутреннее трение.

Пр[ учете в модели потерь возникает целый ряд теоретических и практических трудносчей. Теоретические

; трудности определяютси недостаточной изученностью природы этих потерь и отсутствием хороших моделей. Практические трудности возникают при экспериментальном 01Иределении характеристик потерь.

При выбрре модели учета потерь, а таких моделей существует достаточно много, нужно прежде всего руководствоваться ее применимостью в расчетах вибраций конструкций.

В этом отношении, по-видимому, наиболее подходящей является модель, в которой потери учитываются в виде вязкости.

Что такое вязкость твердого материала?

Чтобы ответить на этот вопрос, вспомним, что такое [.вязкость жидких материалов. Динамической вязкостью ; называется свойство жидкостей или газов, характори-]3ующее их сонротивляемость скольжению или сдвигу. В простейшем случае, когда все слои жидкости движутся параллельно друг другу, сила сопротивления движе-;нию, приходящаяся иа единицу площади в плоскости [слоя, равна коэффициенту вязкости г\, умиожсииому па [градиент скорости в перпендикулярном направлении. [Таким образом, за единицу измерения динамической [вязкости принимается вязкость потока жидкости, в конторой линейная скорость под действием давления сдвига в 1 Па имеет градиент 1 м/с па метр расстояния, пер-1ендикуляриого к плоскости сдвига. В более сложном ;лучае движения жилкости, когда скорости частиц [в разных точках объема не параллельны друг другу, [силы сопротивления движсииео будут иметь различное [направление. Если выделить в жидкости произвольно )риентированную площадку, то силы сопротивления [ожно разложить иа нормальные и касате.чьные к ней, [Отнесенные к единице площади, этн силы называют нор-[мальными и касательными напряжениями в жидкости, соответствии с законом Стокса нормальные и каса-:ельиые напряжения пропорциональны первым произ-юдны.м от деформаций .ю времени. Коэффициентами 1ропорп,иоиальностн служат два коэффициента дииами-геской вязкости tj и %.

Ту же модель можно применить для учета потерь >нергии на внутреннее треиие в твердых телах.

Такое представление потерь удобно уже тем, что уравнения равновесия (3,6) входят напряжения упру-зсти, и ие представляет труда параллельно с каждым 121 129

таким напряжением поставить напряжения (потерь (рис. 3.31):

г.хх

1+ п-

\Xtl -riXtJ

Выразим напряжения потерь через скорости деформаций, используя для коэффициентов ©язкости в твердом теле обозначения и i\, применяемые в гидродинамике для той же цели. Если нормальные упругие напряжения и деформации растяжения (3.5) связаны с помощью дву.\ коэффициентов пропорциональности, то и нормальные напряжения потерь должны выражаться через скорости деформаций с помош.ью двух коэффициентов:

где е -скорости изменения деформаций во времени.

Сразу же заметим, что экспериментальное определение коэффициентов вязкости чрезвычайно сложно: их можно измерить только в динамике, т. е. во время движения. К тому же напряжения потерь неотделимы от упругих напряжений и последние, как правило, гораздо больше по величине. Поэтому коэффициенты вяз1костн твердых тел измеряют косвенно, по затуханию колебаний или по выделяемому во время колебаний теплу. При этом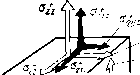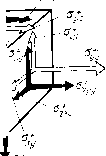

Рмс 3,31.

;тараются избавиться от одного из двух коэффициентов шзкости, строя гипотезы относительно величины и ззаимосвнзи потерь при различных видах деформаций.

Мы также избавимся от одного нз коэфф1г11.иентов. ,ля этого будем считать, что отношение между коэффи-шентами вязкости будет таким же, KaiK между коэф()и-[.иентани упр\тости:

] - 2v (l/2v) -1

(3.29)

Трудно до,казать, что такое соотношение иа самом еле имеет место в твердых телах, ио, во всяком сл.гае, следование этой гипотезе приводит к более точным результатам, чем отбрасывание одного из .коэффициентов вязкости. Для нас же соотношение удо.бно тем, что по-воляег рационально строить расчет[[ую схему.

Вначале выразим первую производную от деформа-ий по времени н виде конечной разности по времени, анее мы указывали, что для повышения порядка ппроксимации первые производные в дифференциаль-ых уравнениях следует заменять центральными разио-тями. Теперь иам сознательно придется понизить поря-ок аппроксимации уравнений движения, взяв в каче-тве первой разности «разность назад».

Если в качестве разности ог деформаций по времени зять «центральную разность»

лг( + Д) ~<хх •) 30

о, поокольку деформации выражаются через перемещения данного и соседних узлов сетки, в уравнениях появятся несколько членов с перемещеинямн на верхнем временном слое {t-\-x). Построить явную схему для расчетов по таким формулам нам не удастся. Если пойти по пути решения задачи с помощью неявной схемы (о не-вных схемах говорится в конце главы), то можно оста-ить при вычислении разности от деформаций и дентальную разность. Но если использовать явную схему, о мы должны вычислять скорость деформаи,нй как [разность назад».

"хх - чх и - (3.31)

Теперь сгруппируем попарно упругие и вязкие иапря-сения, например;

I» 131