коэффициент А одинаков для всех трубок, так как вода Б них одна и та же.

Возьмем два первых потока со знаком плюс и два -вторых со знаком минус и сложим их. В результате получим нуль в полном соответствии с законом сохранения вещества. После сокращения всех членов полученной суммы ,на (AS) и деления на h запишем уравнение движения в виде

{Рт,п Рт+1,п)/ {рт-\,п " Рпг,п)

(1.2)

Зто разностное соотношение для закона сохранения вещества в нашей гидравлической модели, оно будет сира--ведливым для любого внутреннего резервуара, нужно только подставить давление, соответствующие числам т и п. Для резервуаров на границе (т -О, М; п={), N) уравнений записывать не нужно, поскольку давление в этих резервуарах задано.

1.5. Ближе к природе

Рассмотренная гидравлическая модель является искусственной. Такие конструкции в природе не встречаются, хотя процесы фильтрации жидкости через пористые вещества, например через песок, во многом напоминают процессы в нашей модели. Приблизить процессы в модели к движению сплошных масс жидкости без всяких резервуаров можно путем следующих рассуждений. Предположим, что резервуары и трубки имеют прямоугольные формы (рис. 1.8). Чем процессы в такой модели с прямоугольными резервуарами будут отличаться от процессов в модели с круглыми резервуарами? Если течение жидкости достаточно медленное, то ничем. Может несколько измениться коэффициент пропорциональности А. Но в полученном уравнении (1.2) коэффициент А сокращается, и уравнение при переходе к прямоугольным формам не изменится. Теперь будем увеличивать резервуары и трубки, как па рис. 1.9. При каждом таком увеличении изменяется площадь сечения трубок. Но в уравнении (1.2) площадь трубок также сокращается, и уравнение меняться не будет. Размер же резервуаров в наших рассуждениях вообще участия не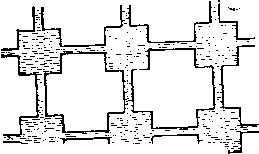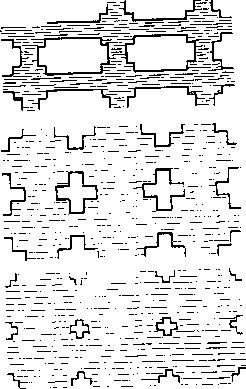

Рис. 1.8.

принимал. Итак, трубки и резервуары растут, перемычки между ними уменьшаются, пока не обратятся в линии, а в трехмерной задаче - в точки. А затем можно убрать и точки,

поскольку они на движении

жидкости не отражаются. - - - ------

Следовательно, уравнение------ ------

(1.2) остается справедливым •riinrtu:ii:rzj?ri:rr: и для сплошных масс жидко- z£TiZE:Z~£?z:Z~£r£r

сти, если только давление по •---•----•----

границам рассматриваемой об- р. 1.9. ласти и величина потоков во

времени не изменяются. Мы выполнили, как говорят, предельный переход от модели с трубками и резервуарами к сплошному потоку жидкости.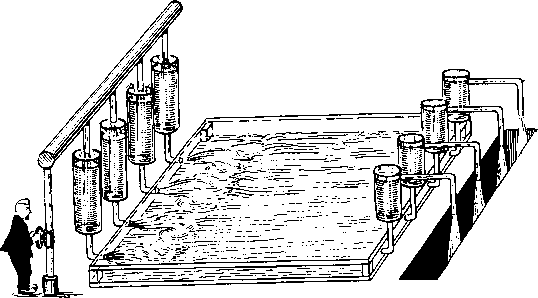

Рис. 1.10. 2*

При предельном переходе к сплошному потоку в плоских задачах нужно подумать о том, что делать с потоками в третьем вертикальном направлении. Нужно позаботиться о том, чтобы потоков воды в вертикальном направлении не было. Этого можно добиться в нашей задаче, если ограничить жидкость двумя горизонтальными плоскостями с небольшим расстоянием между ними (рис. 1.10).

1-6. Вперед - к бесконечно малым!

В плоской модели, показанной на рис. 1.10, нет никакой координатной сетки с шагами /i, разделяющей жидкость на элементарные объемы. Эту сетку мы мысленно дредставляем, чтобы вычислять давление в определенных точках - узлах. Поэтому процесс течения жидкости, а следовательно, и точное решение задачи от выбора сетки зависеть не должны. Но в разностное уравнение (1.2) входят шаги сетки h и можно ожидать, что приближенное решение будет зависеть от шагов сетки. Рассмотрим, как будет изменяться система разностных уравнений при уменьшении шагов.

В нашей задаче непрерывное изменение шага h невозможно, так как длина и ширина области должны быть пропорциональны шагу, поэтому выберем наиболее

2 (/,П

П П W 9 8 7

<3

-3 2 / О

6 /77; J

0 12 3 6 6 7 8 9 Wff fimj

Рис. 1.11. 20

1СТ0Й способ дискретного уменьшения шага h. Будем геньшать шаг в два раза, затем еще в два раза и т. д. рис. 1.11). При этом уже проведенные линии будут сохраняться. Будет изменяться только их номер т или п. \ Возьмем узел (mi=I, п\~\) на пересечении линий при первом разбиении области сеткой. В уравнение (1.2) для этого узла войдут пять значений давления в узлах, отмеченных на рис. 1.11 буквой а. Говорят, что разностный оператор в левой части уравнения (1.2) определен на 5-точечном шаблоне. Внутренних узлов сетки при первом разбиении четыре, поэтому уравнений вида (1.2) будет тоже четыре, и в процессе решения нам нужно будет найти четыре неизвестных давления в четырех внутренних узлах, т. е. решить систему из четырех алгебраических уравнений с четырьмя неизвестными.

Выполним второе разбиение, уменьшив шаги в два раза. В уравнение (1.2) для этого же узла (7П2=2, Пг- =2) войдут теперь пять значений давления в узлах, отмеченных буквой b и расположенных вдвое ближе друг к другу. Теперь сетка будет содержать 25 внутренних узлов и придется решать систему из 25 уравнений с 25 неизвестными.

При третьем разбиении узлы 5-точечного шаблона снова сблизятся: внутренних узлов теперь будет 121. Если продолжить эту процедуру до бесконечности, то вся область покроется узлами-точками, расположенными бесконечно близко по отношению Друг к другу. Число уравнений и число неизвестных также возрастает до бесконечности, а сами уравнения будут дифференциальными уравнениями в частных производных. Разумеется, вид этих уравнений во всех точках области будет одинаковым, и поэтому нужно использовать какое-нибудь одно уравнение. Считают, что оно должно удовлетворяться в любой точке области. Каким будет это уравнение?

Чтобы ответить на этот вопрос, рассмотрим выражения для плотности потоков в направлении оси х и разности плотностей потоков в этом направлении. Выражения для плотностей потоков получаются из уравнений для потоков в трубках 3 п 4 (рис. 1.7), если эти потоки разделить на площадь сечения трубки S:

(71+1 П

)lh.

(1.3)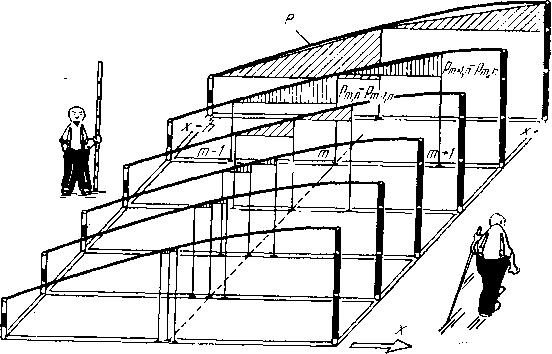

Рис. f.IZ

где знаком « + » отмечен поток, уходящий от узла в на направлении оси х (направо) (рис. 1.7), а знаком «-» - поток, приходящий к узлу слева. Коэффидиеит В характеризует свойства воды и появился вместо коэффициента А при предельном переходе от модели с трубками к сплошному потоку воды.

При измельчении шага сетки !г и числитель, и знаменатель в выражениях (1.3) будут уменьшаться, стремясь в пределе к нулю. Сама дробь -стремится к постоянной величине. Если бы функция Р была известна (рис. 1.12). то разности, входящие в выражения (1.3), определялись бы отношением катетов заштрихованных треугольников. В пределе это отношение стремилось бы к постоянной величине, определяемой тангенсом угла наклона касательной к кривой Р в точке x=m\hu т. е. к производной в точке x-rtiihu

дР дх

(1.4)

Таким образом, обе разности заменяются одной и той 1ке производной. При обратном переходе от производных К разностям можно заменять производные так:

дР и

РтЛ-\,п Рщ.п

1П,П

Рт-1,п

6. -к (1-5)

в первом случае разность называется правой, во втором- левой. В выражениях (1.4) и (1.5) записаны частные производные, а не полные, потому что рассматривается приращение функции Р в направлении одной координаты независимо от ее приращения в другом направлении.

Следовательно, при переходе от дифференциальных уравнений к разностным первые производные можно за-.менять правыми или левыми разностями. Возмол-.ны и другие способы замены. Возникает вопрос: какой из этих способов является лучшим? При разностном решении д11фференциальных уравнений в частных производных основным нсгочником ошибок являются ногрешно--сти от замены п]юизводных конечными разностями. Эти погрешности называют погрешностями дискретизации. Таким образом, в теории разностных схем основной является проблема наилучшего приближения с помощью разностных соотношений к дифференциальным, или наилучшей аппроксимации дифференциальных операторов разности ыми.

1.7. Аппроксимация

Погрешности дискретизации зависят не только от способа замены дифференциальных уравнений разностными, но и от конфигурации элементов конструкции (формы рассматриваемой области), внешних воздействий (граничных условий) и длительности рассчитываемого процесса. Оценка этих погрешностей не менее сложна, чем сам расчет процесса в конструкции.

Если трудно определить погрешности дискретизацшк то довольно просто найти порядок величины этих по грешностей. Порядок погрешностей решения задачи целиком определяется способом замены дифференциальных операторов в задаче разностными, т. v.