Иапрвтчтн Злемепты связей

р. Л

вимсй огИосить к узлу элементы связи, расположенные в нанравленин координатных осей, а элементы, расположенные в иротивополон;-ном направлении, - к соседним узлам в соответствующем ианравлепии. Таким образом, какдому узлу будут принадлежать девять элементов связи для определения коэффициентов Ламе, имеющих верхний индекс с плюсом (рнс. 3.23) и предназначенных для вычисления нормальных напряжений.

Касательные напряжения выражаются через деформации сдвига, а величина каждой деформации определяется с помощью двух углов поворота граней элементов. Следовательно, для определения коэффициентов Ламе при вычислении каждого значения касательного напряжения потребуется два элемента связи, Всего по шести граням элемента массы приложено 12 касательных напряжений н для их вычисления нужно иметь 24 элемента связи. Две]1адцать из них мы отнесем к данному узлу (рис, 3,24), а двенадцать- к соседним узлам, Для коэффициентов )i, с помощью которых вычисляются касательные напряжения, введены те же с>бозначе-ния, что и для коэффициентов i(?. + 2i) и Я, используемых для вычисления нормальных напряжений, ио поскольку нижние индежсы у коэффициентов \\ разные, порядок их записи имеет определенный смысл.

Например, прн вычнсленпн касательного напряжения

aj используются два коэффициента; и \ Первый хоэффициент умножается на угол сдвига, оп1ределясмый изменением перемещения v (первый индекс) вдоль оси л: (второй индекс);

Рис. 3.24.

а второй умножается иа угол, определяемый изменением перемещения и (первый индекс) вдоль направления у (второй индекс):

[и{уЛ-)-\~11 (Л-К yh)-u[y -h) -

-«(x-LA, у~ h)]!hy.

Оба эти угла вычисляются для центра передней лрани элемента массы, поэтому верхние индексы у них одинаковые;

Среди элементов связен, изображенных иа рис. 3,24, имеются одинаковые, однако способы вычаслештя средник значении коэффтоецтов ynpyiOCTH д,чя этих элс-MCirroB могут быть и разные, в зависимости от расположения граиид между различными материалами, входящими в Каждый элемент.

3.10. Осреднение механических характеристик

Теперь задача состоит в том, чтобы заменить неодно-одныс элементы модели однородными, обладающими I ореднем теми же механическими характеристиками, то и неоднородные. Начнем с осреднения илотности р. ля вычисления среднего значения плотнскти необходи-10 сложить массы частей элемента мзссы и разделить на объем элемента;

Масса каждой части элемента ш,- равна произведению плотности на объем этой части [niypiVi], поэтому Выражение для средней плотности можно записать виде

П У!

ножитель Vil (hjiyh.) определяет относительный объ-м части элемент;!, который можно обозначить через la,, огда выражение для среднего значения плотности примет более компактный вид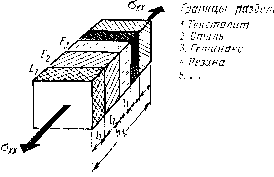

Рис. 3.25.

Вычисление средних значений коэффипиентов упругости несколько сложнее, чем вычисление средней плотности. Средние коэффициенты упругости зависят от расположения граиид раздела между разлилными материалами в элементе связи и от напряжения и вида деформаиии.

Начнем наш анализ с наиболее простого случая, когда в элементе связи границы раздела между материалами проходят параллельно граням элемента (рис. 3.25). Приложим к двум противоположным граням растягивающие напряжения Uxx В этом случае мо.жно считать, что растягивающие напряжения В любом сечении, параллельном передней и задней граням, одинаковы. Зная эти напряжения, можно вычислить деформации каждой части элемента.

Поскольку по остальным граням элемента никаких напряжений ие приложено, относительное удлинение каждой части будет пропорцнональпо растягивающему напряжезпио и обратно пропорционально модулю Юига;

(3.17)

Абсолютное удлинение каждой части будет пропорцио-иальио ее длине: S.li=Z:cx4i- Складывая абсолютные удлинения частей, получают абсолютное удлинение всего элемента связи:

ZJE, t

(3.18)

Относительное удлинение всего элемента, или величина деформации растяжения, будет равна;

Для однородного элемента связь между деформациями растяжения и нормальными напряжениями определяется законом Гука (3.17). Сравнивая выражения (3.17) и (3,19), замечаем, что неоднородный элемент а среднем 5удет растягиваться так же, как и однородный, если :реднсс значение модуля Юига вычислить по формуле

(3.20)

:сли обозначить относительную длину каждой части чс->ез р, то формула для среднего значения модуля Юнга фимет вид

(3.21)

Мы рассмотрели случай, когда направление нормалей к и.тоскостя.м раздела между разны-ми материала.ми I наиравление нормальных напряжений совпадают. Те-lepb рассмотрим случай, -когда нормальные напряжения 1ежат в плоскости раздела (рис, 3.26) к различным ча-тям элемента приложим различные напряжения, чтобы [еформации растяжения частей были одинаковыми. На-тряжение, приложенное к каждой части, определяется хеф ор м а и и е й а с т я ж е н и я

ууг=еууСь (3.22)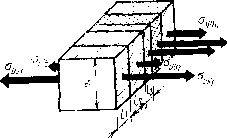

f«c. 3.26,

Вычислим среднее значение напряжений, дейсгнук щих по правой и левой граням элемента связи. Для этот вначале пандем равиоденствующие напряжений, прило женньтх к каждой части:

Затем сунму этих равнодействуютних разделим на площадь грани:

(3.23)

Сравнивая (3.23) с (3.22) для однородного элемент;. получаем для осредиенпого значения модуля Юнга

(3.241

Мы нашли две основные формулы для вычисления средних значений модуля Юнга при растяжении (сжатии) в направлеиии нормали к границам раздела (3.2П и в направлении, параллельном границам (3,24). В пер вом случае среднее значение модуля Юнга будет опре деляться в основном материалом, у которого модул. Юнга наименьший. Например, если одна нз областей представляет собой воддунп1у10 гтроелой:ку между упругими телами и .модуль Юнга ее можно принять равны.м нулю, то еднее знучеиие модуля Юига также будет равно нулю. Во втором случае большее влияние на зе личину среднего значения модуля Юнга оказывает материал с наибольшим модулем Юнга. НапрИхмер, есл)-один из материалов можно считать абсолютно жестким (модуль Юига равен бесконечности), то и среднее зиг; чение модуля Юнга будет равно бесконечности.

Далее можно было бы поставить мысленные эксперн менты для вычисления средних значений коэффициент;! Пуассона. Затем вьгчислить значения деформаций растя ження в случае действия напряжений во всех трех иа правлениях. Уравнения в этом случае пол\1илнсь 6[.i аналогичными выражениям (3.3);

и т. д.

(3.25)

Рошив три уравнения (3,25) относительно папряже НИИ, МЫ получили бы средние значения коэффициентов

аме, которые нам и нужны при составлении уравнений движения. Однако теперь в системе уравнений (3,25) почти (все коэффициенты при наиряжения.х будут различными, и выражения для коэффициентов Ляме сложными и Малопригодными для нрактичеакого пользования.

Можно упростить задачу вычисления средних значений коэффициентов Ламе, если прн вычислении коэ.}>фи-циента Пуассона не учитывать иаправлеиня границ. В реальных материалах, встречающихся в радиоконструкциях, значение коэффицие]1та Пуассона колеблется от 0,3 до 0,4, Это позволяет вычислять среднее значение коэффициента Пуассона так же, как мы вычисляли среднее значение илотности, т. е. учитывать относительный объе;,ц занимаемый каждым материалом:

S*!!* где а, - относительный объем каждого ма-

териала в элементе связи.

Подсчеты показывают, что относительная погрешность от такого упрощения при вычислении коэффиниеп-гов Ламе не превышает 10 ,.. 15% при самом неблагоприятном сочетаиии модулей Юнга и коэффициентов lyaccona различных матертшлов. ЗаметиМ, что это не [огрсшность решения самой задачи расчета вибраций, I только погрешность вычисления упругих характерн-тик отдельных элементов модели. Примерно с такой Х]чиостью модуль Юнга и коэффициент Пуассона опре-еляются экспериментально-После приблнже]ию)-о определения среднего значения :оэффициеита Пуассона решение системы .(3.25) упро-ается, и для средних значений коэффициентов Ламе вьираженнях иормальны.х напряжений получаются сле-ующие формулы:

V-xx

2(1-V)

(3.26)

Средине значеиня коэффициента ji в формулах ка-;ательных напряжений лучше опреде.тять, не прибегая его выражению через £ и v. В этих формулах коэффи-:ент \i.=G является коэффициентом пронорционально-н межд> касательньтмн напряжениями и деформация-1н сдвига (модуль сдвига). Среднее значение модуля .вига вычисляется на основании таких же простых