у поверхности отличны от нуля. Нужно учитывать также, что функция температуры непрерывна и имеет непрерывными первую и вторую производные по координате. Производные могут иметь разрыв, если только в какой-то точке тепловой поток или удельное тепловыделение равны бесконечности, а такого случая быть не может. Кроме того, гипотеза должна отражать однородные свойства пластины и отсутствие источников тепла внутри нее.

Всем этим требованиям удовлетворяет целый ряд гипотез. Например, можно предположить, что температура изменяется по толш,ине пластины по некоторому заданному закону, определяемому суммой заданных аналитических функций координаты. Если в качестве таких составляющих взять степенные функции, то температура представляется в виде разложения в степенной ряд, В этом случае закон изменения температуры в направлении нормали к поверхности можно записать в виде в=во + в1г/+в2г/+ . . . , где 0о, вь &2 и т. д.- некоторые функции, не зависящие от координаты у. Эти функции и предстоит определить в процессе расчета.

При разностном расчете функции во, вь вг, ... должны быть определены в каждом узле плоской модели-сетки. Таким образом, для каждого узла должно быть записано не одно, как ранее, а несколько уравнений. Эти уравнения нам и необходимо вывести.

Если в процессе расчета определены функции во, 0ь &2, .. ., то можно ВЫЧИСЛИТЬ температуру в любой точке по толщине пластины и на ее поверхностях. И тогда задача теплового расчета будет решена. При расчете платы с радиоэлементами их можно расположить в соответствии с распределением температуры по поверхности платы. В местах, которые нагреваются больше, располагаются детали, не критичные к повышению температуры, а в менее нагретых местах можно- радиоэлементы, для которых повышение температуры опасно.

В практике конструирования радиоаппаратуры чаще всего встречается случай, когда разрабатываемая аппаратура предназначается для длительной работы в условиях стабильных внешних воздействий. Тепловой режим в аппарате можно считать установившимся и решать стационарную задачу. Но встречаются случаи, когда аппаратура рассчитывается ца кратковременное вклю-

ЧёИйе или нодвер>кена Непродолжительным теМоЁУМ воздействиям. Тогда конструктора могут интересовать переходные тепловые процессы и приходится решать нестационарную задачу.

Решение стационарной задачи всегда проще, чем нестационарной. Стационарная задача расчета теплового режима в пластинах во многом напоминает приведенный в гл. 1 расчет плоского стационарного течения жидкости. Переход от расчетной схемы для нестационарной задачи к расчетной схеме для стационарной задачи не представляет труда, поэтому мы остановимся на решении нестационарной задачи.

Нам предстоит решить, какое количество членов в разложении температуры в степенной ряд следует сохранить. Разумеется, чтобы расчеты были проще, нужно оставлять меньше число членов. С другой стороны, каждый член разложения несет в себе определенную информацию и, сокращая число членов, можно сильно исказить физическую картину явления и получить большие неконтролируемые погрешности расчета. Рассмотрим физический смысл составляющих температуры 0о, в], ©2. •• (рис. 2.18). Величина во - постоянная по толщине пластины составляющая температуры. Без нее обойтись нельзя, так как не получим изменения средней темпе-[ратуры по поверхности пластины; iei - изменение температуры по толщине пластины по линейному Закону. Эта составляющая нам также необходима, поскольку она определяет величину тепловых потоков в направлении поверхности пластины.

Последующие члены разложения определяют отличие картины распределения температуры от линейного закона. Например, второй член в разложении в степенной ряд является квадратической параболой. Этот член определяет Тот случай, когда происходит быстрое нагревание или охлаждение пластины со стороны ее по-[Срхностей. Например, если пла- рс. 2.18.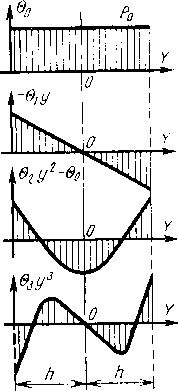

стина одновременно нагревается или охлаждается с обеих сторон, то температура внутри нее может быть выше или ниже, чем на поверхностях.

Таким образом, второй и последующие члены разложения определяют распределение температуры внутри пластины при быстром ее нагревании или охлаждении ее поверхностей. Эти члены мы учитывать не будем, поскольку распределение температуры внутри пластины при тепловых расчетах радиоконструкций нас, как правило, не интересует. Важно знать распределение температуры по поверхности, где могут быть расположены радиоэлементы, чувствительные к изменению температуры.

Таким образом, мы ограничимся в разложении только двумя членами:

в==0о + в1г/. (2.23)

Уравнения для определения функций во и 61 нам и предстоит получить.

Функции температуры во и в1 имеют различную размерность: К и К/м соответственно. В связи с этим в расчетах они могут принимать сильно отличающиеся друг от друга значения. Чтобы избежать большого разброса величин и тем самым уменьшить погрешности округления можно переписать уравнение (2.23) в виде

~ (2.24)

9 = 9о + 9.

где h - половина толщины пластины.

Теперь функции в имеют смысл составляющих температуры на поверхности пластины. Например, при y=h, 0=во + в1; при y=-h, в=во-©Г, во и 0i будут иметь размерность температуры.

Разумеется, значения величин 0о и в1 нам неизвестны. В нашу задачу и входит вычисление их для различных точек на поверхности пластины. Зная распределение температуры по поверхности, можно найти приближенные значения температуры и внутри пластины, используя формулу (2.24).

2.11. От трехмерной сетки к двухмерной

Используя формулу (2.24), заменяем одну неизвестную величину 0 двумя неизвестными 0о и 0ь исключив тем самым из расчетных соотношений координату у,

Исключить координату молено двумя способами. Первый является традиционным и представляет собой интегральное преобразование. Он состоит в том, что в дифференциальных уравнениях в частных производных для трехмерной нестационарной задачи производится подстановка (2.24). Затем интегрируют полученное уравнение по толщине пластины в пределах от -h до -f ft и получают первое уравнение для определения нулевой составляющей температуры 0о. Потом умножают калдый член дифференциального уравнения на у и вновь интегрируют по толщине пластины. В результате получается второе уравнение для определения первой составляющей ©ь Полученные таким образом уравнения являются дифференциальными и содержат частные производные по х и г и времени t. Для построения разностной схемы следует перейти к разностным уравнениям, применяя обычную замену частных производных конечными разностями.

Второй способ позволяет произвести это преобразование уравнений непосредственно в разностной форме. Воспользуемся этим вторым способом.

Начнем с того, что построим для пластины трехмерную модель-сетку (рис. 2.19) с одинаковыми шагами

Рис. 2.19.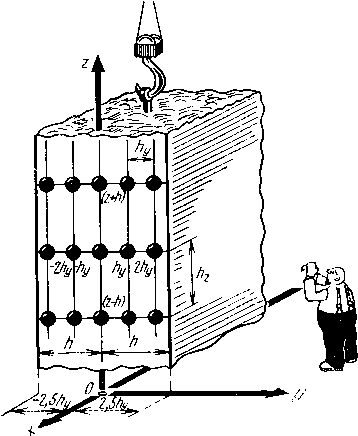

и hz. По толщине пластины возьмем всего пять узлов, чтобы математические выкладки не были слишком громоздкими, В дальнейшем распространим вывод на любое число узлов по толщине пластины. Для произвольной цепочки узлов в направлении у запишем разностные уравнения Фурье (2.9), заменив в них потоки в направлении X я Z через разности от температуры по координатам в соответствии с формулами (2,10). При записи уравнений учтем, что индекс / теперь принимает пполне определенные значения: -2, -1, О, 1, 2.

Уравнения будут иметь вид

1,-2, ft+1 (, -2, k i, -2, k-l

t, -2, k

I,-2,ft

+л(в; . -29! , )=9+

».».*+! i.o.k i.o.k-i i,0,

Л(9 , -20 4-9 4=0

" (2.25)

i,i,k

9 / ,1

i,2,k

/.2.fr+l 1,2,ft i,2,k-l " i,2,k

В радиоконструкциях пластины, как правило, выполняются из одного материала, т. е. рассматриваемая область однородна. Шаги сетки в направлении х vl z мы взяли одинаковыми, поэтому коэффициенты Ах и Az также равны; обозначим их буквой А. Источников тепла в пластине нет, поэтому величину удельного тепловыделения Q мы положили Рис. 2.20. равной нулю.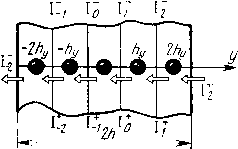

в уравнениях (2.25) сохранились плотности тепловых потоков в направлении оси у. Для них мы оставили то же обозначение, что. и в формулах (2.8), только опустили индекс у и вместо него поставили номер узла в направлении оси у. В дальнейшем нужно будет учесть, что плотности потоков относятся к интервалу между узлами, т. е. к той грани элемента, через которую они проходят.

у элемента с узлом y=-2hy левая площадь грани выходит на поверхность пластины, поэтому плотность потока I]J2 определяется внешним тепловым потоком, падающим на левую поверхность пластины (рис. 2.20). Сдругой стороны, плотность потока 17 Г проходит ;че-pes 1Правую"грань .крайнего правого элемента/у, -Л, поэтому эта плотность" ткже определяетсявнешним

! тепловым потоком, падающим на правую поверхность

! пластины.

В формулах (2.25) получились различные обозначения одних и тех же внутренних тепловых потоков. Например,

в первое уравнение (2.25) входит плотность потока V-

] Это поток, проходящий через правую грань элемента -2Л, j Во второе уравнение (2.25) входит плотность потока iZi • Это поток, проходящий через левую грань элемента - Л. Поскольку эта грань является общей для соседних элементов - 2Л и - hy, то 1;;2 -i являются разными обозначениями одной и той же плотности потока. Следовательно, можно записать

1+ = Г

-2 - I

1+,= 1

Т-. т+ у-

(2.26)

Теперь все величины температуры, входящие в уравнения (2.25), следует выразить через составляющие температуры на поверхности пластины в соответствии с (2.24) и сложить все уравнения (2.25). Сложить их [можно почленно. Например, сумма всех первых членов в первых скобках будет равна

/ + 1.-2»й"Г /-H.-i,ft4 /-и.о.

i-f 1 ,-i,ft "

o,i-l-i,ft