2.9. Более сложные границы

Не всегда удается расположить узлы сетки to4ii( на Гранине раздела между двумя теплопроводящим! средами, В этом случае также можно пользоватыя полученными выше формулами, только вычисление осреднснпых значений коэффициента теплопроводности несколько услол<няется.

Если Гранина представляет собой плоскость, -ю встречается Л1".;) типа элементов связей между узлами В первом случае потоки тепла распространяются парал лельно границе {рис. 2.13). Прн этом потоки, проходи щие по частям элемента, складываются:

Осредпенное значение коэффициента теплопроводно сти получается сложением коэффициентов теплопрово i ности члстси элемнта, пропорциональных ширине эти\ частей:

где CLljhy-, aijh.

(2.20}

Формулу (2.20) можно распространить на случай лю бого числа параллельгиях границ в одном элементе.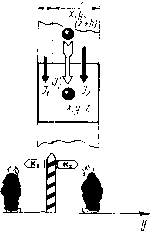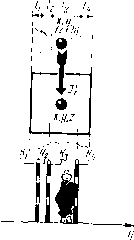

Рис, 2.13.

Рис, 2,14.

<kdi:s>

2.15.

Рис, 2,16,

[И потоки тепла проходят параллельно границам 1С. 2.14):

,=.«. + . + .«, + /.«.-

Во втором случае потоки тепла распросфаняются )мально к поверхности раздела (рис, 2.15). Прн этом кичина плотности потока в любом есчонпп, парал-IbHOM границе, будет одинаковой. Ее можно выразить величины перепада температур, как мы это де-1И в формулах (2.5). С другой стороны, величину )тности потока можно записать Ч1рез осреднснное 1чеиие коэффициента теплопрозодностн:

«1 г °2

(2.21)

рмулу (2.21) легко распространи гь на слуиай любого (ичества параллельных границ:

вр К, "1"/С. К,

Радиоинженерам более привычны электрические ве-1ЧИНЫ, чем тепловые, поэтому им полезно сравнить Ьмулы (2.20) и (2,21) с формулами для нараллель-Г0 и последовательного соединения сопротивлений электрических цепях (рис. 2.16). При сравнении нуж-иметь в виду, что коэффициент теплопроводности [яется аналогом удельной электропроводности. Используя последовательно формулы (2.20) и (2.21), шо вычислить приближенное значение осредненного

коэффициента теплопроводности для элемента практически любой сложности. Покажем это на примере. Предположим, что после разбивки блока на элементы в каком-го элементе связи оказалось три области, которые мы услошю назовем «транзистор», «плата» и «наполнитель» (рнс. 2.17). На рисунке показаны зна-1ення коэффициентов теплопроводности частей элемента и их размеры. Заменим криволинейную поверхность транзистора плоскостями, параллельными координатным плоскостям, и разобьем элемент на однородные части (рис. 2,17),

Вначале по формуле (2.21) определяется осредненное значение коэффициента теплопроводности для первой и второй частей элемента. При этом коэффициенты пропорциональности

ai--0,02I/(0,02l-hO,0!2)=0,64, 02 = 0,012/(0,021 + 0,012) =0,36,

а значение осредненного коэффициента теплопроводности

Кср=ОМ 58 -1 - 0,36 -0,11 =-37,1.

Затем по формуле (2.22) вычисляют коэффициент для всего элемента. При этом коэффициенты пропорцио-иальности

ai-=0,0G5/(0,005 + 0,0l8 + 0,0l3)=0,l4, a2=0,0I8/(0,005-f 0,018 + 0.013) =0,50, аз=0,013/(0,005 + 0,018 + 0,0!3)=0,36,

Значение осреднспиого коэффициента теплопроводности для всего элемента

1 0,14 , 0,50 , 0,36

О-з+ЙТТ+зХТ=-0™-Ь 4,167 + 0,010.

0,21

/(,„Н0,21 Дж/(м-с-К).

При таком способе вычисления коэффициентов теп-1 лопроводности может оказаться, что в уравнениях двп-Ження (2.10) все шесть коэффициентов окажутся разными н, разумеется, отличными от коэффициентов в уравнениях для других узлов. В этом случае значения коэффициентов нужно хранить в памяти ЦВМ. Требуе-Г.мын объем памяти резко возрастает. При этом нужно [учитывать, что каждый коэффициент является общим [для двух соседних узлов. Поэтому всего коэффициентов будет в три, а нс в шесть раз больше, чем узлов.

Удельная теплоемкость осреднястся по объему эле-; мента массы, в центре которого находится узел сетки, [Предположим, что элемент массы состоит нз нескольких частей, в которые входят материалы с удельной Теплоемкостью Сь Сг, Сз, ,.. Объем, занимаемый каж-[дым материалом в элементе массы, будет равен соответственно Va, V3, ... Тогда количество теплоты, {Накапливаемой в каждой части элемента, опре-[делится произведением i=:CiVAO; 2=С22Дв; цъ= вСзКзДЭ, ,.. А общее количество теплоты, иаканли-кВаемое элементом массы, будет = (C1V1 + C2V2 + г,4-СзУз+. ..) ДО. Прн замене неоднородного элемента {однородным со средней теплоемкостью Сер количество теплоты должно остаться прежним; g = Ccx,hxhyhzA©. ")тсюда значение средней теплоемкости можно опреде-[лить так:

(2.22)

Для каждого элемента массы в неоднородном блоке [РЭА может получиться свой коэффициент осредненной [Теплоемкости. Это потребует дополнительного объема

памяти ЦВМ для хранения коэффициентов М (2.13), [Таких коэффициентов будет столько же, сколько и узлов i сетки.

Прн выполнении операции осреднения характеристик [атериалов мы предполагали, что величина теплового Ютока в каждой части неоднородного элемента связи не

меняется по объему этой части, а нрнращсиие теМйв ратуры AG не меняется по объему элемента массы. На самом деле это величины, изменяющиеся от точки к точке. Это приводит к появлению дополнительных погрешностей. Однако эти предположения по сути дела совпадают с предположениями, которые заложены в основе иывода разностны.ч уравнений. Поэтому «погрешности осреднения» будут того же порядка, что и погрешности дискретизации.

2.10. Где тонко...

В радиоконструкциях применяется много деталей из листовых материалов (печатные платы, кожухи, шасси, магнитные и тепловые экраны). Эти детали играют существенную роль в процессах теплопередачи в конструкции, и поэтому расчеты тепловых потоков, проникающих через них и распределяющихся в плоскости деталей, представляют большой практический интерес.

Если для таких деталей при разностных расчетах строить трехмерную модель-сетку по принципу, изложенному выше, то возникают две трудности: во-первых, в модели получается очень много узлов и возрастает объем вычислений, во-вторых, шаги сетки н направлении нормали к поверхности детали получаются очень маленькими. В свою очередь, малые шаги по координате приводят к необходимости уменьшения и шагов по времени, иначе решение с помощью явной схемы будет неустойчивым. Причем между шагом по координате и шагом по времени из условия устойчивости получается квадратическая зависимость, Если шаг по координате уменьшается в 10 раз, то шаг по времени нужно уменьшить в 100 раз. Это, в свою очередь, приводит к увеличению объема вычисленпй.

В то же время плоские детали (пластипы) позволяют строить для них плоские модели-сетки. В такой модели по толщине пластины берется всего один узел и сетка получается двухмерной. Это приводит к уменьшению числа узлов и сокращению объема вычислений и снимает трудности, связанные с малыми шагами по координате нормальной к поверхности пластины,

Разумеется, для расчетов тепловых потоков с помощью такой двухмерной модсли-сстки потребуются другие расчетные формулы, отличные от тех, которые 70

мы получили выше, Далее мы перейдем к выводу расчетных соотношений для расчетов распределения температуры в плоских деталях типа пластин.

При переходе от трехмерной задачи к двухмерной необходимо из расчетных соотношений исключить одну

.независимую переменную. Поскольку расчет при этом значительно упрощается, этим приемом постоянно поль-

-зуются как при точных, так и при численных методах. Однако исключение одной переменной возможно далеко не всегда. Такая возможность появляется только тогда, когда задача в целом обладает некоторыми свойствами симметрии. Например, если решается осесимметричная задача для тел пилнидрической формы, то, применяя цилиндрическую систему координат, можно исключить одну переменную - угол и останется только две координаты- в направлении оси цилиндра и в направлепин радиуса. Решение задач со сферической симметрией можно свести к решению одномерных задач, применяя сферическую систему координат.

В нашем случае детали имеют прямоугольные формы, поэтому система координат должна остаться прямоугольной. В прямоугольной системе исключение од-

iHOH координаты можно произвести на основании некоторой гипотезы о поведении искомых функций в направлении этой координаты. Выбор той или иной гипотезы

определяется в каждом конкретном случае в зависимости от формы области и граничных условий. Если, например, теплопроводящая пластина помещена между .двумя теилонзоляпионными прокладками, то естественно предположить, что тепловые потоки в направлении нормали к поверхности отсутствуют и температура по толщине пластины постоянна. В этом случае нужно исключить из расчетных соотношений соответствующие тепловые потоки, и уравнение будет двухмерным, Мы уже пользовались этим приемом прн рассмотрении по-.токов воды между двумя параллельными пластинами,

В радиоконструкциях тепловая изоляция на поверх-Щостп пластин, как правило, отсутствует, и тепловые отоки в направлении поверхности нельзя считать рав-ыми нулю. Нужна иная гипотеза относительно распре-делеиия температуры по толщине пластины. Эта гипо-еза должна учитывать наличие тепловых потоков на оверхиостях и, следовательно, то, что температура и ее .роизводиая по нормали к поверхности должны быть