
 |
| Главная -> Книги (0) (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) ( 15 ) (16) (17) (18) (19) (20) (21) (22) (23) (24) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) (51) (52) (53) (54) (55) (56) (57) (58) (59) (60) (61) (62) (63) (64) (65) (66) (67) (68) (69) (70) (71) (72) (73) (74) (75) (76) (77) (78) (79) (80) (81) (82) (83) (84) (85) (86) (87) (88) (89) (90) (91) (92) (93) (94) (95) (96) (97) (98) (99) (100) (15) по 5 П4 9 П5 ИПО БП 11 ИП1 С/П ПО С/П П1 ИПО + S ~ КП4 ИПО ИП1 - 8 КП5 ИП4 9 - х=0 08 ИП6 ИП7 + П2 ИП6 ИП7 - П4 ИП8 ИП9 + ПЗ ИПЗ ИП9 - П5 ИПА ИПВ - П6 ИПА ИПВ + П8 ИПС ИПД - П7 ИПС ИПД + П9 ИП2 ИПЗ + ПО ИП2 ИПЗ - П1 ИП4 ИП5 - П2 ИП4 ИП5 + ПЗ ИП6 ИП7 + П4 ИП6 ИП7 - П5 ИП8 ИП9 - П6 ИПЗ ИП9 + П7 С/П Инструкция. 40) = РХ В/О С/П РХ = х(0), 41) = PX С/П РХ = 41), х(2) = РХ С/П ... х{7) = РХ С/П РО = Оо, Р1 = сц, Р2 = Ог, . .., Р7 = РХ=а,; -<<30 с. Пример. Для = 0; 1; 2; 3; 4; 5; 6; 7 получим Оо = 3,5, а, =-2, 02=0, 03 = -1, 04 = 0; Об = 0; Og = 0; о, = -0,5. Программы ДПФ и БПФ с комплексным представлением отсчетов преобразуемых функций применимы для прямого и обратных преобразований при соответствующем изменении знака поворачивающего множителя в (2.5). 2.3. Спектральный анализ непрерывных сигналов Если необходимо проанализировать спектр непрерывного сигнала, заданного аналитическим (буквенным) выражением, а выполнить интегрирование в замкнутом виде ие удается, то приходится прибегать к численным методам спектрального анализа. Один из них основан на предельном соотношении X (jo)) = lim X (jv) 8 в->-<х. между спектрами непрерывного сигнала и полученного из него путем дискретизации (с интервалом 8) сигнала, ДПФ которого дает дискретные приближенные значения искомой спектральной функции. При этом следует учитывать, что для сигналов x(t) со спектром, ограниченным значением /в при 7":1/(2/в), спектральная функция х(]\) отображает дискретные точечные значения спектральной функции х{]ш). Практическая реализация рассматриваемого метода состоит из следующих этапов: 1. Построение табличной модели анализируемой функции x{t) при выбранном интервале дискретизации 8, что можно выполнить с помощью программы вычисления этой функции с шагом 6 аргумента. 2. Выполнение ДПФ полученной табличной модели в предположении, что она является моделью сигнала с огибающей x(t), по программам, приведенным в § 2.2. 3. Денормировка вычисленных значений спектральной функции согласно соотношениям x(]oi) = x(ikQ) x(iv)Q, (2.15) где П = 2л/8 для непериодических сигналов. 48 Комплексные амплитуды составляющих спектра периодического сигнала (при выборке от=Г/6, равной целому числу) Cfc=2x(jv)e/T=2;c(jv)/т, (2.16) где Г-период анализируемого сигнала. При реализации рассмотренного алгоритма особого внимания требует выбор интервала дискретизации, обеспечивающий заданную точность анализа при минимальных затратах времени. В этом случае строгая оценка методической погрещностн является сложной задачей, и необходимо максимально использовать имеющуюся информацию о реальной щирине спектра анализируемого сигнала. Так, для «простых» сигналов* граничная частота спектра fmax»k/x, где т-длительность сигнала, а * -коэффициент, определяемый его формой и равный единицам или десяткам единиц. Выбор е упрощается, если задана полоса анализируемых частот. В этом случае 6=1/(2/тах). но по мере приближения к граничной частоте fmax погрещ-ность вычисления х{]и>) для сигналов, щирина спектра которых превыщает /max, резко возрастает. Если при анализе спектров периодических сигналов для ДПФ выбирают m = T/Q. то для непериодических сигналов т следует выбирать по значению частот (i) = kQ, на которых вычисляют хЦш), связанных с интервалом дискретизации и числом т обрабатываемых отсчетов функции x{i) соотнощеии-ем Q=l/(m6). Если для финитных функций величину Qmax определяют числом ненулевых отсчетов, то при введении дополнительных нулевых отсчетов значение Q можно сделать сколь угодно малым. В качестве примера определим спектральную плотность прямоугольного импульса x{t) = \ при 0<<т=1 мкс и x(t)=0 при 0>/>Т иа частотах, кратных 250 кГц. Полагая реальную щирииу спектра примерно равной 4 МГц, выберем интервал дискретизации б = 1/(2/в) =0,125 мкс. Чтобы получить отсчеты спектральной функции на заданных частотах, соответствующих спектральным составляющим периодического сигнала с периодом 7"= 1 (250-10) =4 мкс, найдем ДПФ решетчатой функции, заданной т= 4/0,125 = 32 отсчетами, из которых 1/0,125 = 8 будут равны единице, а остальные нулю. Воспользовавшись для этого сигнала результатами ДПФ, выполненного в § 2.2, после денорми-ровки получим следующие значения: х(]ш) ; д:()250 кГц) =9,017641 • 10" (точное значение 9,003162-10); лг(]500 кГц) =6,407288-10 (точное значение 6,366197Х ХЮ); jc(j750 кГц) =3.044885-10- (точное значение 3,001054-10-); ... Если т велико, то полный спектральный анализ связан с большими затра тами времени и предпочтительнее может оказаться метод, основанный иа аппроксимации анализируемой функции x(t). позволяющей выполнить преобразование (2.1) и получить формулу, с достаточной точностью описывающую спектр анализируемого сигнала. Например, при кусочио-лииейиой аппроксимации О при / < <1, ai(/ - <i)-t-Pi при !i<<<<2, X {().:{...... . (2.17) «к C - th) +h при < г < /ft-f 1, О при th+i < t Варакии Л. Е. Теория сложных сигналов. - М.: Сов. радио, 1970-376с. после интегрирования по (2.1) находим 1= 1 где коэффициенты S, = ai-a, i, а Л( = Рг-а, ,(<,-отличны от нуля только при наличии у функции x(t) разрывов первого рода. Заметим, что при вычислении значений А\ и Bi следует принять ао = Ро=0. Коэффициенты At и В, можно вычислить непосредственно по отсчетам функции x(t). Программа 39. Вычисление коэффициентов приближенной спектральной функции ПЗ П2 П4 Сх П5 С/П П6 П7 1 С/П П8 - П9 ИП2 ИП7 - ШЗ ИП6 ПЗ - ~ ПА ИП5 - ПВ ИПА П5 ИП8 П2 ИПВ ИП4 ИП9 П4 БП 06 Инструкция. 4<i) = pY, <1 = РХ В/О С/П РХ = 0, x(<2) = PY, <2=РХ С/П (если функция имеет разрыв в очередной точке, то, например, x(t2-Q)=PY, ti = РХ С/П РХ = x{t - 0), х(2 + 0) = РХ) С/П РХ = Лг, РУ = Si ... С/П РХ = /1д, ,, РУ = В,, ,, ,-0) = РУ, =РХ С/П РХ = х(<,-0), x((k+1 + 0) = РХ С/П РХ = Л*, РУ = В* ... x(tr) = РУ, = РХ С/П РХ = = x(tr), 0 = РХ С/П РХ = Л ,, РУ =В 1, 0 = РУ, = РХ С/П РХ = 0 С/П PX=i4r, PY=Br (где г -конец последнего участка аппроксимации, - произвольное зиачеине, удовлетворяющее условию ts>tr). В качестве примера для временной характеристики, аппроксимированной кусочио-линейиой функцией (рис. 7, а), выполняем: 10 В О В/О С/П (РХ = 0) 8 Bf 5 С/П (РХ=8) 2 /-/ С/П PX=10=i, PY = -0,4=Bi; О Bf 10 С/П (РХ=0) С/П РХ=-10=Л2, РУ=0,8=В2; О Bf 20 С/П (РХ=0) С/П РХ= =0 = Лз, РУ = -0,4==Вэ. Следовательно, A:(jo))= -(-0,4 + jlOco -f (0,8 - jl0u))e-JS*>-f.( 0,4)e-J"")x X(u-=((0,4 + 0,4cosl0co -0,8cos5(u + 10(osin5(o)-f j(10(acos5(tt - lOco+0,8siп5<й- -0,4sin 10u)))/a)2. xCt) X(tr0) 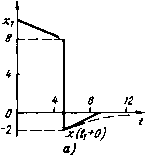 \x(w)\ 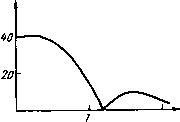 2 <y Рис. 7 (0) (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) ( 15 ) (16) (17) (18) (19) (20) (21) (22) (23) (24) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) (51) (52) (53) (54) (55) (56) (57) (58) (59) (60) (61) (62) (63) (64) (65) (66) (67) (68) (69) (70) (71) (72) (73) (74) (75) (76) (77) (78) (79) (80) (81) (82) (83) (84) (85) (86) (87) (88) (89) (90) (91) (92) (93) (94) (95) (96) (97) (98) (99) (100) |
|
|